Advertisements
Advertisements
प्रश्न
Consider a wire carrying a steady current, I placed in a uniform magnetic field B perpendicular to its length. Consider the charges inside the wire. It is known that magnetic forces do no work. This implies that ______.
- motion of charges inside the conductor is unaffected by B since they do not absorb energy.
- some charges inside the wire move to the surface as a result of B.
- if the wire moves under the influence of B, no work is done by the force.
- if the wire moves under the influence of B, no work is done by the magnetic force on the ions, assumed fixed within the wire.
पर्याय
b and c
a and d
b and d
c and d
उत्तर
b and d
Explanation:
If a current carrying straight conductor (length l) is placed in a uniform magnetic field (B) such that it makes an angle θ with the direction of field, then the force experienced by it is Fmax= Bil sin θ. Direction of this force is obtained by the right-hand palm rule.
Right-hand palm rule: Stretch the fingers and thumb of the right hand at right angles to each other. Then if the fingers point in the direction of field B and thumb in the direction of current z, then normal to the palm will point in the direction of force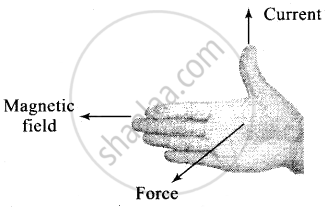
If conductor is placed perpendicular to magnetic field, then θ = 90°, Fmax = Bil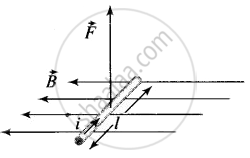
APPEARS IN
संबंधित प्रश्न
A circular coil carrying a current I has radius R and number of turns N. If all the three, i.e. the current
I, radius R and number of turns N are doubled, then, the magnetic field at its centre becomes:
(a) Double
(b) Half
(c) Four times
(d) One fourth
Obtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I
A circular coil of N turns and radius R carries a current I. It is unwound and rewound to make another coil of radius R/2, current I remaining the same. Calculate the ratio of the magnetic moments of the new coil and original coil.
A charge ‘q’ moving along the X- axis with a velocity `vecv` is subjected to a uniform magnetic field B along the Z-axis as it crosses the origin O.
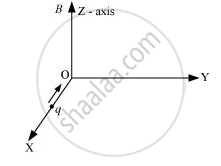
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
A charged particle would continue to move with a constant velocity in a region wherein ______.
- E = 0, B ≠ 0.
- E ≠ 0, B ≠ 0.
- E ≠ 0, B = 0.
- E = 0, B = 0.
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
A beam of light travelling along X-axis is described by the electric field Ey = 900 sin ω(t - x/c). The ratio of electric force to magnetic force on a charge q moving along Y-axis with a speed of 3 × 107 ms-1 will be : [Given speed of light = 3 × 108 ms-1]
Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
Lorentz force in vector form is ______.
