Advertisements
Advertisements
प्रश्न
Obtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I
उत्तर
Magnetic flux density B at the centre of a circular coil of radius r having N turns and carrying a current I.
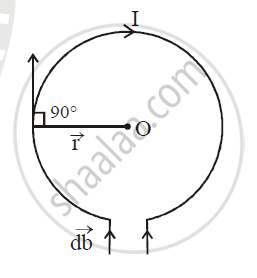
Consider a circular coil of radius r and carrying the current I in the direction as shown in the figure. Suppose the entire circular coil is divided into a large number of current elements, each of length dl. According to Biot-savart law, the magnetic field `vec(dB)` at the centre O of the coil due to current element `Ivec(dl)` is given by
`vec(dB) = mu_0/(4pi) (I(vec(dl) xx vecr))/r^3`
The magnitude of `vec(db)` at the centre O is
`dB = mu_0/(4pi) (Idl xx r sin theta)/(r^3)`
`db = mu_0/(4pi) (I dl sin theta)/r^2`
`.B = int dB`
`= int mu_0/(4pi) (i dl sin theta)/r^2`
`theta= 90^@` `∴ sin 90^@ = 1`
`:. B = mu_o/(4pi) I/r^2 int dldl`
`intdl`= total length of the coil = `2pir`
`B = mu_o/(4pi) I/r^2 (2pir)`
`B =(mu_oI)/(2r)`
If the coil N turns
`:. B = (mu_oNI)/(2r)`
APPEARS IN
संबंधित प्रश्न
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
Deduce the expression for the magnetic field at a point on the axis of a current carrying circular loop of radius ‘R’ distant ‘x’ from the centre. Hence, write the magnetic field at the centre of a loop.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
Magnetic lines of force always cross each other
Explain the term hysteresis
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
Which of the following particles will experience maximum magnetic force (magnitude) when projected with the same velocity perpendicular to a magnetic field?
A charged particle is moved along a magnetic field line. The magnetic force on the particle is
Choose the correct alternative and rewrite the following:
What will happen to the current passing through a resistance, if the potential difference across it is doubled and the resistance is halved?
A charged particle is in motion having initial velocity `vecv` when it enters into a region of uniform magnetic field perpendicular to `vecv`. Because of the magnetic force the kinetic energy of the particle will ______.
According to the right-hand rule, the direction of magnetic induction if the current is directed in an anticlockwise direction is ______
A very high magnetic field is applied to a stationary charge. Then the charge experiences ______.
- perpendicular to direction of velocity of charged particle.
-
perpendicular to direction of magnetic field.
-
parallel to direction of velocity of charged particle.
-
parallel to the direction of magnetic field.
Which one of the following is a correct statement about magnetic forces?
A circular current loop of magnetic moment M is in an arbitrary orientation in an external magnetic field B. The work done to rotate the loop by 30° about an axis perpendicular to its plane is ______.
A charged particle would continue to move with a constant velocity in a region wherein ______.
- E = 0, B ≠ 0.
- E ≠ 0, B ≠ 0.
- E ≠ 0, B = 0.
- E = 0, B = 0.
With a neat labelled diagram, explain cyclotron motion and cyclotron formula.
Distinguish between the forces experienced by a moving charge in a uniform electric field and in a uniform magnetic field. (Any two points)
