Advertisements
Advertisements
प्रश्न
Obtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I
उत्तर
Magnetic flux density B at the centre of a circular coil of radius r having N turns and carrying a current I.
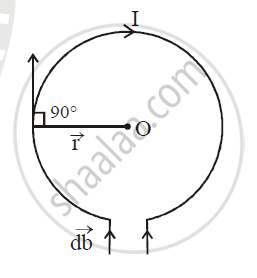
Consider a circular coil of radius r and carrying the current I in the direction as shown in the figure. Suppose the entire circular coil is divided into a large number of current elements, each of length dl. According to Biot-savart law, the magnetic field `vec(dB)` at the centre O of the coil due to current element `Ivec(dl)` is given by
`vec(dB) = mu_0/(4pi) (I(vec(dl) xx vecr))/r^3`
The magnitude of `vec(db)` at the centre O is
`dB = mu_0/(4pi) (Idl xx r sin theta)/(r^3)`
`db = mu_0/(4pi) (I dl sin theta)/r^2`
`.B = int dB`
`= int mu_0/(4pi) (i dl sin theta)/r^2`
`theta= 90^@` `∴ sin 90^@ = 1`
`:. B = mu_o/(4pi) I/r^2 int dldl`
`intdl`= total length of the coil = `2pir`
`B = mu_o/(4pi) I/r^2 (2pir)`
`B =(mu_oI)/(2r)`
If the coil N turns
`:. B = (mu_oNI)/(2r)`
APPEARS IN
संबंधित प्रश्न
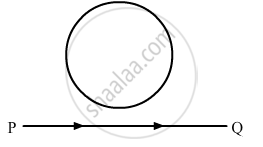
A conducting loop is held above a current carrying wire PQ as shown in the figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constantly increasing.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
A circular coil carrying a current I has radius R and number of turns N. If all the three, i.e. the current
I, radius R and number of turns N are doubled, then, the magnetic field at its centre becomes:
(a) Double
(b) Half
(c) Four times
(d) One fourth
Define one tesla using the expression for the magnetic force acting on a particle of charge q moving with velocity \[\vec{v}\] in a magnetic field \[\vec{B}\] .
A steady current (I1) flows through a long straight wire. Another wire carrying steady current (I2) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I1 exerts a magnetic force on the second wire. Write the expression for this force.
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
A charged particle is moved along a magnetic field line. The magnetic force on the particle is
The force between two parallel current-carrying conductors is F. If the current in each conductor is doubled, then the force between them becomes ______
If a particle of charge 1012 coulomb moving along the `hat"x" -` direction with a velocity 102 m/s experiences a force of 1 o-s newton in `hat"y" -` direction due to magnetic field, then the minimum magnetic field is ____________.
A proton enters into a magnetic field of induction 1.732 T, with a velocity of 107 m/s at an angle 60° to the field. The force acting on the proton is e = 1.6 × 10-19 C, sin 60° = cos 30° = `sqrt3/2`
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
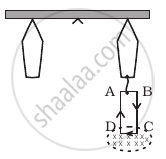
A 100 turn rectangular coil ABCD (in XY plane) is hung from one arm of a balance (Figure). A mass 500 g is added to the other arm to balance the weight of the coil. A current 4.9 A passes through the coil and a constant magnetic field of 0.2 T acting inward (in xz plane) is switched on such that only arm CD of length 1 cm lies in the field. How much additional mass ‘m’ must be added to regain the balance?
Two conducting rails are connected to a source of emf and form an incline as shown in figure. A bar of mass 50 g slides without friction down the incline through a vertical magnetic field B. If the length of the bar is 50 cm and a current of 2.5 A is provided by battery. Value of B for which the bar slide at a constant velocity ______ × 10-1 Tesla. 2 [g = 10 m/s2]

Figure shows a square loop. 20 cm on each side in the x-y plane with its centre at the origin. The loop carries a current of 7 A. Above it at y = 0, z = 12 cm is an infinitely long wire parallel to the x axis carrying a current of 10 A. The net force on the loop is ______ × 10-4 N.
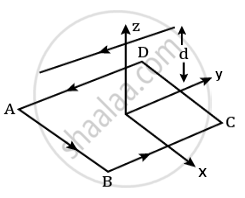
An electron is moving along positive x-axis in a magnetic field which is parallel to the positive y-axis. In what direction will the magnetic force be acting on the electron?
Two long parallel current-carrying conductors are 0.4 m apart in air and carry currents 5 A and 10 A. Calculate the force per metre on each conductor, if the currents are (a) in the same direction and (b) in the opposite direction.
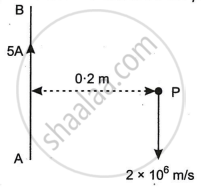
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.