Advertisements
Advertisements
प्रश्न
Explain "Magnetic force never does any work on moving charges".
उत्तर
- Magnetic force is given by `vec"F"_"m" = "q"(vec"v" xx vec"B")`.
- This makes direction of magnetic force `(vec"F"_"m")` perpendicular to direction of velocity of charged particles `(vec"v")`.
- Thus, the magnetic force is in turn perpendicular to the displacement of charged particles.
- According to properties of the dot product, `vec"F"_"m".vec"v" = 0,` for any magnetic field `vec"B"`.
Hence, magnetic force never does any work on moving charges.
APPEARS IN
संबंधित प्रश्न
Seema’s uncle was advised by his doctor to have an MRI (Magnetic Resonance Imaging) scan of his brain. Her uncle felt it to be expensive and wanted to postpone it. When Seema learnt about this, she took the help of her family and also approached the doctor, who also offered a substantial discount. She then convinced her uncle to undergo the test to enable the doctor to know the condition of his brain. The information thus obtained greatly helped the doctor to treat him properly.
Based on the above paragraph, answer the following questions:
(a) What according to you are the values displayed by Seema, her family and the doctor?
(b) What could be the possible reason for MRI test to be so expensive?
(c) Assuming that MRI test was performed using a magnetic field of 0.1 T, find the minimum and maximum values of the force that the magnetic field could exert on a proton (charge = 1.6 x 10-19 C) moving with a speed of 104 m/s.
Explain the term hysteresis
A circular coil of N turns and radius R carries a current I. It is unwound and rewound to make another coil of radius R/2, current I remaining the same. Calculate the ratio of the magnetic moments of the new coil and original coil.
A steady current (I1) flows through a long straight wire. Another wire carrying steady current (I2) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I1 exerts a magnetic force on the second wire. Write the expression for this force.
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
A straight horizontal wire of mass 10 mg and length 1.0 m carries a current of 2.0 A. What minimum magnetic field B should be applied in the region, so that the magnetic force on the wire may balance its weight?
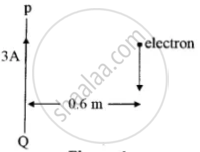
PQ is a long straight conductor carrying a current of 3A as shown in Figure below. An electron moves with a velocity of 2 x 107 ms-1 parallel to it. Find the force acting on the electron.
Choose the correct alternative and rewrite the following:
What will happen to the current passing through a resistance, if the potential difference across it is doubled and the resistance is halved?
A charged particle is in motion having initial velocity `vecv` when it enters into a region of uniform magnetic field perpendicular to `vecv`. Because of the magnetic force the kinetic energy of the particle will ______.
The force between two parallel current-carrying conductors is F. If the current in each conductor is doubled, then the force between them becomes ______
A magnetic field set up using Helmholtz coils is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 × 10–5 V m–1, make a simple guess as to what the beam contains. Why is the answer not unique?
Lorentz Force generally refers to ______.
A deuteron of kinetic energy 50 keV is describing a circular orbit of radius 0.5 metre in a plane perpendicular to the magnetic field B. The kinetic energy of the proton that describes a circular orbit of radius 0.5 metre in the same plane with the same B is ______.
- perpendicular to direction of velocity of charged particle.
-
perpendicular to direction of magnetic field.
-
parallel to direction of velocity of charged particle.
-
parallel to the direction of magnetic field.
The magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as ______.
What is the magnetic induction of the field at the point O in a current I carrying wire that has the shape shown in the figure? The radius of the curved part of the wire is R, the linear parts are assumed to be very long.

A magnetic field exerts no force on
The phenomenon in which a magnetic field is produced in the space near a conductor carrying current is called ______
In the product
`overset(->)("F") = "q"(overset(->)(υ) xx overset(->)("B"))`
= `"q"overset(->)(υ) xx ("B"overset(^)("i") + "B" overset(^)("j") + "B"_0overset(^)("k"))`
For q = 1 and `overset(->)(υ) = 2overset(^)("i") + 4overset(^)("j") + 6overset(^)("k")` and
`overset(->)("F") = 4overset(^)("i") - 20overset(^)("j") + 12overset(^)("k")`
What will be the complete expression for `overset(->)("B")`?
Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B = B0k̂.
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
Show that a force that does no work must be a velocity dependent force.
A charged particle of charge e and mass m is moving in an electric field E and magnetic field B. Construct dimensionless quantities and quantities of dimension [T]–1.
A long straight conductor kept along X' X axis, carries a steady current I along the +x direction. At an instant t, a particle of mass m and charge q at point (x, y) moves with a velocity `vecv` along +y direction. Find the magnitude and direction of the force on the particle due to the conductor.
Distinguish between the forces experienced by a moving charge in a uniform electric field and in a uniform magnetic field. (Any two points)
