Advertisements
Advertisements
Question
Explain "Magnetic force never does any work on moving charges".
Solution
- Magnetic force is given by `vec"F"_"m" = "q"(vec"v" xx vec"B")`.
- This makes direction of magnetic force `(vec"F"_"m")` perpendicular to direction of velocity of charged particles `(vec"v")`.
- Thus, the magnetic force is in turn perpendicular to the displacement of charged particles.
- According to properties of the dot product, `vec"F"_"m".vec"v" = 0,` for any magnetic field `vec"B"`.
Hence, magnetic force never does any work on moving charges.
APPEARS IN
RELATED QUESTIONS
Use this law to find magnetic field due to straight infinite current carrying wire.
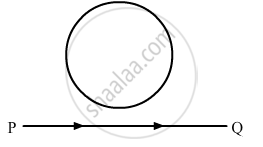
A conducting loop is held above a current carrying wire PQ as shown in the figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constantly increasing.
A rod of length l is moved horizontally with a uniform velocity 'v' in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
Magnetic lines of force always cross each other
A circular coil carrying a current I has radius R and number of turns N. If all the three, i.e. the current
I, radius R and number of turns N are doubled, then, the magnetic field at its centre becomes:
(a) Double
(b) Half
(c) Four times
(d) One fourth
Obtain an expression for magnetic flux density B at the centre of a circular coil of radius R, having N turns and carrying a current I
A charge ‘q’ moving along the X- axis with a velocity `vecv` is subjected to a uniform magnetic field B along the Z-axis as it crosses the origin O.
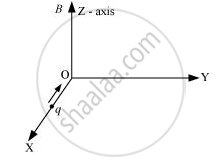
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
A straight wire carrying an electric current is placed along the axis of a uniformly charged ring. Will there be a magnetic force on the wire if the ring starts rotating about the wire? If yes, in which direction?
A straight horizontal wire of mass 10 mg and length 1.0 m carries a current of 2.0 A. What minimum magnetic field B should be applied in the region, so that the magnetic force on the wire may balance its weight?
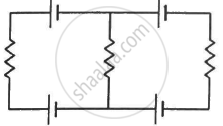
Each of the batteries shown in figure has an emf equal to 5 V. Show that the magnetic field B at the point P is zero for any set of values of the resistances.
An electron is moving with a speed of 3.2 × 107 m/s in a magnetic field of 6.00 × 10-4 T perpendicular to its path. What will be the radium of the path? What will be frequency and the energy in keV?
[Given: mass of electron = 9.1 × 10−31 kg, charge e = 1.6 × 10−19 C, 1 eV = 1.6 × 10−19 J]
Show that currents in two long, straight, parallel wires exert forces on each other. Derive the expression for the force per unit length on each conductor.
A charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other. The particle will move in a ____________.
A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? (g = 9.8 m s–2)
The magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as ______.
A magnetic field exerts no force on
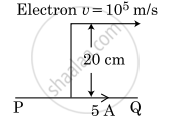
An infinitely long straight conductor carries a current of 5 A as shown. An electron is moving with a speed of 105 m/s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B = B0k̂.
The magnetic force depends on v which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that the net acceleration has a different value in different frames of reference?
A charge particle moves along circular path in a uniform magnetic field in a cyclotron. The kinetic energy of the charge particle increases to 4 times its initial value. What will be the ratio of new radius to the original radius of circular path of the charge particle:
Two long current-carrying conductors are placed parallel to each other at a distance of 8 cm between them. The magnitude of the magnetic field produced at the mid-point between the two conductors due to the current flowing in them is 300µT. The equal current flowing in the two conductors is ______.
Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
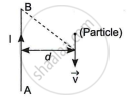
A long straight wire AB carries a current I. A particle (mass m and charge q) moves with a velocity `vec"v"`, parallel to the wire, at a distance d from it as shown in the figure. Obtain the expression for the force experienced by the particle and mention its directions.
An electron is moving along positive x-axis in a magnetic field which is parallel to the positive y-axis. In what direction will the magnetic force be acting on the electron?
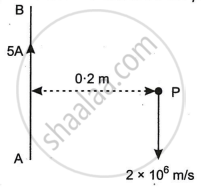
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.