Advertisements
Advertisements
Question
Use this law to find magnetic field due to straight infinite current carrying wire.
Solution
Magnetic field due to straight infinite current carrying wire:
The figure below shows a straight infinite current carrying wire around which a circular loop of radius r is shown
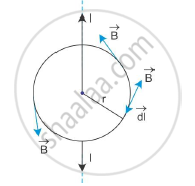
The field lines are circular, and hence, the field B at any point of the circular loop is directed along the tangent to the circle at that point. The magnitude of field B is the same at every point of the circular loop.
Therefore, we get
∫B.dl=∫Bdl cosθ = ∫Bdl cos0 = B∫dl =B(2πr)
Now, from Ampere’s circuital law, the above equation is
`B(2pir)=mu_0I`
`:.B=(mu_0I)/(2pir)`
APPEARS IN
RELATED QUESTIONS
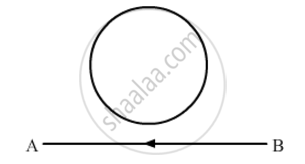
The electric current flowing in a wire in the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
Which of the following particles will experience maximum magnetic force (magnitude) when projected with the same velocity perpendicular to a magnetic field?
A charged particle is moved along a magnetic field line. The magnetic force on the particle is
A proton enters into a magnetic field of induction 1.732 T, with a velocity of 107 m/s at an angle 60° to the field. The force acting on the proton is e = 1.6 × 10-19 C, sin 60° = cos 30° = `sqrt3/2`
A very high magnetic field is applied to a stationary charge. Then the charge experiences ______.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
A cubical region of space is filled with some uniform electric and magnetic fields. An electron enters the cube across one of its faces with velocity v and a positron enters via opposite face with velocity – v. At this instant ______.
- the electric forces on both the particles cause identical accelerations.
- the magnetic forces on both the particles cause equal accelerations.
- both particles gain or loose energy at the same rate.
- the motion of the centre of mass (CM) is determined by B alone.
A long straight conductor kept along X' X axis, carries a steady current I along the +x direction. At an instant t, a particle of mass m and charge q at point (x, y) moves with a velocity `vecv` along +y direction. Find the magnitude and direction of the force on the particle due to the conductor.
