Advertisements
Advertisements
Question
Currents of equal magnitude pass through two long parallel wires having a separation of 1.35 cm. If the force per unit length on each of the wires is 4.76 x 10-2 N, what must be I ?
Solution 1
Data: l1 = I2 = l, s = 1.35 x 10-2
F = `(mu_0/(4pi)) (2"I"_1"I"_2l)/"s" = (mu_0/(4pi)) (2"I"^2l)/"s"`
∴ `"I"^2 = "F"/"I" "s"/(2(mu_0//4pi))`
`= (4.76 xx 10^-2) (1.35 xx 10^-2)/(2 xx 10^-7) = 3.213 xx 10^3`
∴ I = `sqrt(32.13 xx 10^2)` = 56.68 A
Solution 2
Given:
I1 = I2 = I, `"F"/"L"` = 4.76 × 10-2 N
d = 1.35 cm = 1.35 × 10-2 m
To find: Electric current
Formula:
`"F"/"L" = (mu_0"I"_1"I"_2)/(2pi"d")`
Calculation:
From formula,
`4.76 xx 10^-2 = (4pi xx 10^-7 xx "I" xx "I")/(2 xx pi xx 1.35 xx 10^-2)`
∴ I2 = `(4.76 xx 10^-2 xx 1.35 xx 10^-2)/(2 xx 10^-7) = 1.35 xx 2.38 xx 10^{-2-2+7}`
I = `sqrt(1.35 xx 2.38 xx 10^3)`
= `sqrt(13.5 xx 2.38) xx 10`
= `{"anti log"(1/2(log 13.5 + log 2.38))} xx 10`
= `{"anti log"(1/2(1.1303 + 0.3766))} xx 10`
= {antilog (0.7535)} × 10
= 5.669 × 10
= 56.69 A
The electric current is 56.69 A.
APPEARS IN
RELATED QUESTIONS
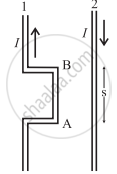
Two wires shown in the figure are connected in a series circuit and the same current of 10 A passes through both, but in opposite directions. The separation between the two wires is 8 mm. The length AB is 22 cm. Obtain the direction and magnitude of the magnetic field due to current in wire 2 on the following figure segment AB of wire 1. Also, obtain the magnitude and direction of the force on wire 1. [μ0 = 4π × 10-7 T.m/A]
Two long parallel wires, both carrying current I directed into the plane of the page, are separated by a distance R. Show that at a point P equidistant from the wires and subtending an angle θ from the plane containing the wires, the magnitude of the magnetic field is B = `(mu_0)/pi "I"/"R"` sin 2θ. What is the direction of the magnetic field?
A very long straight wire carries a current of 5.2 A. What is the magnitude of the magnetic field at a distance 3.1 cm from the wire?
The magnetic field at a distance of 2.4 cm from a long straight [current-carrying] wire is 16 µT. What is the current through the wire?
The figure shows a cylindrical wire of diameter a, carrying a current I. The current density in the wire is in the direction of the axis and varies linearly with radial distance r from the axis according to the relation J = `"J"_0 "r"/"a"`. Obtain a magnetic field B inside the wire at a distance r from its center.

In the problem, what will be the magnetic field B inside the wire at a distance r from its center, if the current density J is uniform across the cross-section of the wire? Figure shows a section of a very long cylindrical wire of diameter a, carrying a current I. The current density which is in the direction of the central axis of the wire varies linearly with radial distance r from the axis according to the relation J = Jo r/a.

Derive the expression for magnetic field produced by a current in a circular arc of wire.
A length L of wire carries a steady current I. It is bent first to form a circular plane coil of one turn. The same length is now bent more sharply to give a double loop of smaller radius. The magnetic field at the centre caused by the same current is ______.
Two concentric circular coils of six turns each are situated in the same plane. Their radii are 10 cm and 20 cm and they carry respectively 0.1 A and 0.2 A current in same direction. The magnetic field in tesla at the centre is ______.
The ratio of the magnetic field at the centre of a current-carrying circular wire and the magnetic field at the centre of a semi-circular coil made from the same length of wire will be ______.
A circular coil 'A' has a radius 'R' and the current flowing through it is I. Another circular coil 'B' has radius 4R and current flowing through it is 4I. The magnetic field at the centre of the circular coil is in the ratio of ______.
lf the current flowing in a circular loop is in clockwise direction, then the magnetic induction will be ____________.
The magnetic induction at the centre of a coil made from a wire of length 44 m carrying a current of 0.5 A is nearly ____________.
A wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is ____________.
When a certain length of wire is turned into one circular loop, the magnetic induction at the centre of coil due to current 'I' flowing through it is B1. If the same wire is turned into four loops to make a circular coil, the magnetic induction at the centre of this coil is 'B2' for same current then relation between B2 and B1 is ____________.
A circular arc of radius 'r' carrying current 'I' subtends on angle `pi/16` at its centre. The radius of a metal wire is uniform. The magnetic induction at the centre of circular arc is ____________.
A wire of length 'L' carries current 'I' along the x-axis, A magnetic field B = B0 `(hat "i" - hat "j" - hat "k")` T acts on the wire. The magnitude of the magnetic force acting on the wire is ____________.
Two concentric circular coils having radii r1 and r2, (r2 << r1) are placed co-axially with centers coinciding. The mutual induction of the arrangement is (Both coils have a single turn) (µ0 = permeability of free space).
Two concentric circular coils of 'n' turns each are situated in the same plane. Their radii are 'a1' and 'a2' (a2 > a1) and they carry currents 'I1' and 'I2' respectively (I1> I2) in opposite direction. The magnetic field at the centre is ____________.
