Advertisements
Advertisements
Question
The figure shows a cylindrical wire of diameter a, carrying a current I. The current density in the wire is in the direction of the axis and varies linearly with radial distance r from the axis according to the relation J = `"J"_0 "r"/"a"`. Obtain a magnetic field B inside the wire at a distance r from its center.

Solution
dI = JdA = `("J"_0"r"/"a") = 2 pi "rdr" = (2pi"J"_0"r"^2"dr")/"a"` .....(1)
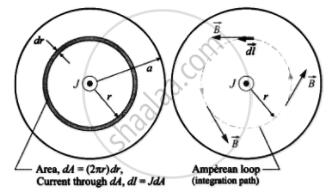
When we apply Ampere's circuital law to the circular path of integration, we see that the wire has perfect cylindrical symmetry, with all charges moving parallel to the wire. As a result, the magnetic field must be tangent to circles concentric with the wire. The enclosed current is the current that is enclosed within radius r. Thus,
`oint "Bdl" = mu_0"I"_"encl"`
`therefore oint "Bdl" = mu_0 int_0^"r" "dl" = mu_0 int_0^"r" (2pi"J"_0)/"a" "r"^2 "dr"` ....(2)
`therefore "B"(2pi"r") = (mu_0 2pi"J"_0)/"a" ("r"^3/3)`
`therefore "B" = (mu_0 "J"_0)/"3a" "r"^2` ....(3)
which is the required expression.
APPEARS IN
RELATED QUESTIONS
Currents of equal magnitude pass through two long parallel wires having a separation of 1.35 cm. If the force per unit length on each of the wires is 4.76 x 10-2 N, what must be I ?
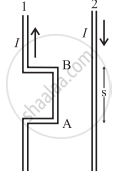
Two wires shown in the figure are connected in a series circuit and the same current of 10 A passes through both, but in opposite directions. The separation between the two wires is 8 mm. The length AB is 22 cm. Obtain the direction and magnitude of the magnetic field due to current in wire 2 on the following figure segment AB of wire 1. Also, obtain the magnitude and direction of the force on wire 1. [μ0 = 4π × 10-7 T.m/A]
A very long straight wire carries a current of 5.2 A. What is the magnitude of the magnetic field at a distance 3.1 cm from the wire?
The magnetic field at a distance of 2.4 cm from a long straight [current-carrying] wire is 16 µT. What is the current through the wire?
In the problem, what will be the magnetic field B inside the wire at a distance r from its center, if the current density J is uniform across the cross-section of the wire? Figure shows a section of a very long cylindrical wire of diameter a, carrying a current I. The current density which is in the direction of the central axis of the wire varies linearly with radial distance r from the axis according to the relation J = Jo r/a.

Derive the expression for magnetic field produced by a current in a circular arc of wire.
An electron moving in a circular orbit of radius r makes n rotations per second. The magnetic field produced at the centre has magnitude ____________.
A length L of wire carries a steady current I. It is bent first to form a circular plane coil of one turn. The same length is now bent more sharply to give a double loop of smaller radius. The magnetic field at the centre caused by the same current is ______.
Two concentric circular coils of six turns each are situated in the same plane. Their radii are 10 cm and 20 cm and they carry respectively 0.1 A and 0.2 A current in same direction. The magnetic field in tesla at the centre is ______.
The ratio of the magnetic field at the centre of a current-carrying circular wire and the magnetic field at the centre of a semi-circular coil made from the same length of wire will be ______.
A circular coil 'A' has a radius 'R' and the current flowing through it is I. Another circular coil 'B' has radius 4R and current flowing through it is 4I. The magnetic field at the centre of the circular coil is in the ratio of ______.
lf the current flowing in a circular loop is in clockwise direction, then the magnetic induction will be ____________.
The magnetic induction at the centre of a coil made from a wire of length 44 m carrying a current of 0.5 A is nearly ____________.
A wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is ____________.
When a certain length of wire is turned into one circular loop, the magnetic induction at the centre of coil due to current 'I' flowing through it is B1. If the same wire is turned into four loops to make a circular coil, the magnetic induction at the centre of this coil is 'B2' for same current then relation between B2 and B1 is ____________.
A wire of length 'L' carries current 'I' along the x-axis, A magnetic field B = B0 `(hat "i" - hat "j" - hat "k")` T acts on the wire. The magnitude of the magnetic force acting on the wire is ____________.
Two concentric circular coils having radii r1 and r2, (r2 << r1) are placed co-axially with centers coinciding. The mutual induction of the arrangement is (Both coils have a single turn) (µ0 = permeability of free space).
Two concentric circular coils of 'n' turns each are situated in the same plane. Their radii are 'a1' and 'a2' (a2 > a1) and they carry currents 'I1' and 'I2' respectively (I1> I2) in opposite direction. The magnetic field at the centre is ____________.
