Advertisements
Advertisements
Question
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.
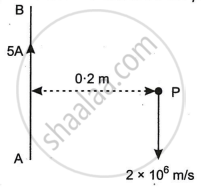
Solution
The magnetic field due to the current carrying wire is perpendicular to the plane of the paper, in a downward direction.
i.e., `vec"B" = - (mu_0"I")/(2pi"d") vec"k"`
Force `vec "F" = q vecv xx vec"B"`
`= e(- v vec"j") xx (- (mu_0"I")/(2pi"d") vec"k")`
`= (mu_0ev"I")/(2pi"d") vec "i"`
Given that d = 0.2 m, ν = 2 × 106 m/s, I = 5 A
`therefore "F" = (mu_0"e" xx 2 xx 10^6 xx 5 xx 10^5)/(2pi xx 0.2) vec"i"`
`= (2 xx 10^-7 xx 1.6 xx 10^-19 xx 2 xx 10^6 xx 5 xx 10^5)/0.2`
`= 160 xx 10^-13` N
APPEARS IN
RELATED QUESTIONS
(a) Write the expression for the magnetic force acting on a charged particle moving with velocity v in the presence of magnetic field B.
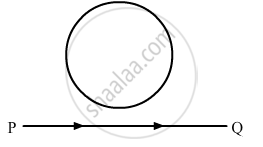
A conducting loop is held above a current carrying wire PQ as shown in the figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constantly increasing.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?
Explain the term hysteresis
A circular coil of N turns and radius R carries a current I. It is unwound and rewound to make another coil of radius R/2, current I remaining the same. Calculate the ratio of the magnetic moments of the new coil and original coil.
The free electrons in a conducting wire are in constant thermal motion. If such a wire, carrying no current, is placed in a magnetic field, is there a magnetic force on each free electron? Is there a magnetic force on the wire?
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
A charged particle is released from rest in a region of steady and uniform electric and magnetic fields which are parallel to each other. The particle will move in a ____________.
A very high magnetic field is applied to a stationary charge. Then the charge experiences ______.
Direction of magnetic force on a positive charge moving in a magnetic field is given by ______.
Correct unit of magnetic field is ______.
Assertion: Free electrons always keep on moving in a conductor even then no magnetic force act on them in magnetic field unless a current is passed through it.
Reason: The average velocity of free electron is zero.
The magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as ______.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
A circular current loop of magnetic moment M is in an arbitrary orientation in an external magnetic field B. The work done to rotate the loop by 30° about an axis perpendicular to its plane is ______.
An electron enters with a velocity v = v0i into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the electron is found to spiral down inside the cube in plane parallel to the x-y plane. Suggest a configuration of fields E and B that can lead to it.
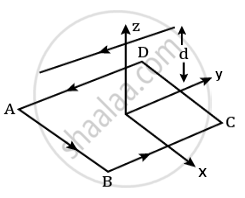
Figure shows a square loop. 20 cm on each side in the x-y plane with its centre at the origin. The loop carries a current of 7 A. Above it at y = 0, z = 12 cm is an infinitely long wire parallel to the x axis carrying a current of 10 A. The net force on the loop is ______ × 10-4 N.
A unit vector is represented as `(0.8hat"i" + "b"hat"j" + 0.4hat"k")`. Hence the value of 'b' must be ______.
Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
