Advertisements
Advertisements
प्रश्न
A straight horizontal wire of mass 10 mg and length 1.0 m carries a current of 2.0 A. What minimum magnetic field B should be applied in the region, so that the magnetic force on the wire may balance its weight?
उत्तर
Given:
Mass of the wire, M = 10 mg = 10−5 Kg
Length of the wire, l = 1.0 m
Electric current flowing through wire, I = 2.0 A
As per the question, the weight of the wire should be balanced by the magnetic force acting on the wire.Also angle between the length of the wire and magnetic field is 90°
Thus, Mg = IlB, where
g is the acceleration due to gravity = 9.8 m/s2
B is the applied magnetic field
So,
`B = (Mg)/(Il)`
= `(10^-5xx9.8)/(2xx1)`
= 4.9 ×10-5 T
APPEARS IN
संबंधित प्रश्न
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
Use this law to find magnetic field due to straight infinite current carrying wire.
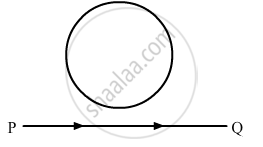
A conducting loop is held above a current carrying wire PQ as shown in the figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constantly increasing.
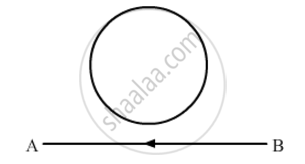
The electric current flowing in a wire in the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
A charge ‘q’ moving along the X- axis with a velocity `vecv` is subjected to a uniform magnetic field B along the Z-axis as it crosses the origin O.
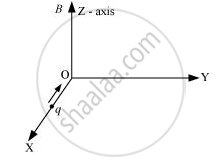
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
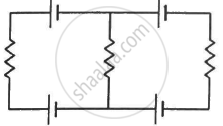
Each of the batteries shown in figure has an emf equal to 5 V. Show that the magnetic field B at the point P is zero for any set of values of the resistances.
Write the expression for the Lorentz force F in vector form.
State whether the following statement is true or false:
Magnetic poles exist in pairs.
According to the right-hand rule, the direction of magnetic induction if the current is directed in an anticlockwise direction is ______
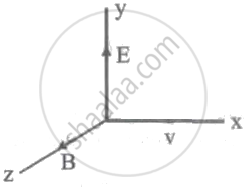
A particle with charge q moves with a velocity v in a direction perpendicular to the directions of uniform electric and magnetic fields, E and B respectively, which are mutually perpendicular to each other. Which one of the following gives the condition for which the particle moves undeflected in its original trajectory?
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = `0.72 (μ_0"NI")/"R"` approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
In the product
`overset(->)("F") = "q"(overset(->)(υ) xx overset(->)("B"))`
= `"q"overset(->)(υ) xx ("B"overset(^)("i") + "B" overset(^)("j") + "B"_0overset(^)("k"))`
For q = 1 and `overset(->)(υ) = 2overset(^)("i") + 4overset(^)("j") + 6overset(^)("k")` and
`overset(->)("F") = 4overset(^)("i") - 20overset(^)("j") + 12overset(^)("k")`
What will be the complete expression for `overset(->)("B")`?
A charged particle would continue to move with a constant velocity in a region wherein ______.
- E = 0, B ≠ 0.
- E ≠ 0, B ≠ 0.
- E ≠ 0, B = 0.
- E = 0, B = 0.
The magnetic force depends on v which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that the net acceleration has a different value in different frames of reference?
A beam of light travelling along X-axis is described by the electric field Ey = 900 sin ω(t - x/c). The ratio of electric force to magnetic force on a charge q moving along Y-axis with a speed of 3 × 107 ms-1 will be : [Given speed of light = 3 × 108 ms-1]
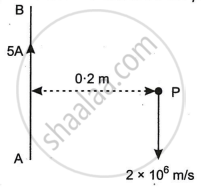
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.