Advertisements
Advertisements
प्रश्न
Write the expression for the Lorentz force F in vector form.
उत्तर
`vec"F" = "q"(vec"V" xx vec"B" + vec"E")` - Notation have usual meaning, `vec"F"` is the total force experienced by a moving charged particle in a magnetic field `vec"B"` and electric field `vec"E"`.
APPEARS IN
संबंधित प्रश्न
Deduce the expression for the magnetic field at a point on the axis of a current carrying circular loop of radius ‘R’ distant ‘x’ from the centre. Hence, write the magnetic field at the centre of a loop.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
The net charge in a current-carrying wire is zero. Then, why does a magnetic field exert a force on it?
A straight wire carrying an electric current is placed along the axis of a uniformly charged ring. Will there be a magnetic force on the wire if the ring starts rotating about the wire? If yes, in which direction?
Two wires carrying equal currents i each, are placed perpendicular to each other, just avoiding a contact. If one wire is held fixed and the other is free to move under magnetic forces, what kind of motion will result?
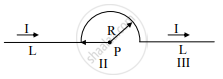
A conductor has three segments; two straights of length L and a semicircular with radius R. It carries a current I What is the magnetic field B at point P?
Explain "Magnetic force never does any work on moving charges".
The magnetic moment is NOT associated with ____________.
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = `0.72 (μ_0"NI")/"R"` approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?
Direction of magnetic force on a positive charge moving in a magnetic field is given by ______.
- If v is parallel to B, then path of particle is spiral.
- If v is perpendicular to B, then path of particle is a circle.
- If v has a component along B, then path of particle is helical.
- If v is along B, then path of particle is a circle.
The correct plot of the magnitude of magnetic field `vec"B"` vs distance r from centre of the wire is, if the radius of wire is R.
In the product `vec"F" = "q" (vec"υ" xx vec"B")`
= `"q" vec"υ" xx ("B"hat"i" +"B"hat"j" + "B"_0hat"k")`
For q = 1 and `vec"υ" = 2hat"i" + 4hat"j" + 6hat"k"` and
`vec"F" = 4hat"i" - 20hat"j" + 12hat"k"`
What will be the complete expression for `vec"B"`?
A circular current loop of magnetic moment M is in an arbitrary orientation in an external magnetic field B. The work done to rotate the loop by 30° about an axis perpendicular to its plane is ______.
Two long current-carrying conductors are placed parallel to each other at a distance of 8 cm between them. The magnitude of the magnetic field produced at the mid-point between the two conductors due to the current flowing in them is 300µT. The equal current flowing in the two conductors is ______.
With a neat labelled diagram, explain cyclotron motion and cyclotron formula.
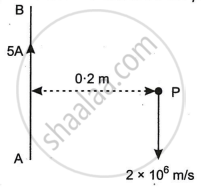
A long straight wire AB carries a current of 5A. P is a proton travelling with a velocity of 2 × 106 m/s, parallel to the wire, 0.2 m from it and in a direction opposite to the current, as shown in Figure below. Calculate the force which magnetic field of the current carrying conductor AB exerts on the proton.