Advertisements
Advertisements
प्रश्न
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = `0.72 (μ_0"NI")/"R"` approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
उत्तर
Radius of circular coil = R
Number of turns on the coil = N
Current in the coil = I
Magnetic field at a point on its axis at distance x is given by the relation,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
Where,
μ0 = Permeability of free space
(a) If the magnetic field at the centre of the coil is considered, then x = 0.
∴ B = `(μ_0"IR"^2"N")/(2"R"^3) = (μ_0"IN")/(2"R")`
This is the familiar result for magnetic field at the centre of the coil.
(b) Radii of two parallel co-axial circular coils = R
Number of turns on each coil = N
Current in both coils = I
Distance between both the coils = R
Let us consider point Q at distance d from the centre.
Then, one coil is at a distance of `"R"/2 + "d"` from point Q.
∴ Magnetic field at point Q is given as:
B1 = `(μ_0"NIR"^2)/(2[("R"/2 + "d")^2 + "R"^2]^(3/2))`
Also, the other coil is at a distance of `"R"/2 - "d"` from point Q.
∴ Magnetic field due to this coil is given as:
B2 = `(μ_0"NIR"^2)/(2[("R"/2 - "d")^2 + "R"^2]^(3/2))`
Total magnetic field,
B = B1 + B2
= `(μ_0"IR"^2)/2 [{("R"/2 - "d")^2 + "R"^2}^(3/2) + {("R"/2 + "d")^2 + "R"^2}^(3/2)]`
= `(μ_0"IR"^2)/2 [((5"R"^2)/4 + "d"^2 - "Rd")^(3/2) + ((5"R"^2)/4 + "d"^2 + "Rd")^(3/2)]`
= `(μ_0"IR"^2)/2 xx ((5"R"^2)/4)^(3/2) [(1 + 4/5 "d"^2/"R"^2 - 4/5 "d"/"R")^{3/2) + (1 + 4/5 "d"^2/"R"^2 + 4/5 "d"/"R")^(3/2)]`
For d << R, neglacting the factor `"d"^2/"R"^2`, we get:
`≈ (μ_0"IR"^2)/2 xx ((5"R"^2)/4)^(3/2) xx [(1 - (4"d")/(5"R"))^(3/2) + (1 + (4"d")/(5"R"))^(3/2)]`
`≈ (μ_0"IR"^2"N")/(2"R"^3) xx (4/5)^(3/2) [1 - (6"d")/(5"R") + 1 + (6"d")/(5"R")]`
B = `(4/5)^(3/2) (μ_0"IN")/"R" = 0.72 ((μ_0"IN")/"R")`
Hence, it is proved that the field on the axis around the mid-point between the coils is uniform.
APPEARS IN
संबंधित प्रश्न
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
Magnetic lines of force always cross each other
A particle of charge ‘q’ and mass ‘m’ is moving with velocity .`vecV` It is subjected to a uniform magnetic field `vecB` directed perpendicular to its velocity. Show that it describes a circular path. Write the expression for its radius.
Which of the following particles will experience maximum magnetic force (magnitude) when projected with the same velocity perpendicular to a magnetic field?
The correct plot of the magnitude of magnetic field `vec"B"` vs distance r from centre of the wire is, if the radius of wire is R.
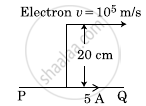
An infinitely long straight conductor carries a current of 5 A as shown. An electron is moving with a speed of 105 m/s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant.
Consider a wire carrying a steady current, I placed in a uniform magnetic field B perpendicular to its length. Consider the charges inside the wire. It is known that magnetic forces do no work. This implies that ______.
- motion of charges inside the conductor is unaffected by B since they do not absorb energy.
- some charges inside the wire move to the surface as a result of B.
- if the wire moves under the influence of B, no work is done by the force.
- if the wire moves under the influence of B, no work is done by the magnetic force on the ions, assumed fixed within the wire.
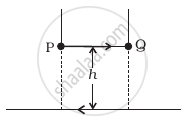
A long straight wire carrying current of 25 A rests on a table as shown in figure. Another wire PQ of length 1 m, mass 2.5 g carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise?
Two long parallel current-carrying conductors are 0.4 m apart in air and carry currents 5 A and 10 A. Calculate the force per metre on each conductor, if the currents are (a) in the same direction and (b) in the opposite direction.
