Advertisements
Advertisements
Question
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = `0.72 (μ_0"NI")/"R"` approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
Solution
Radius of circular coil = R
Number of turns on the coil = N
Current in the coil = I
Magnetic field at a point on its axis at distance x is given by the relation,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
Where,
μ0 = Permeability of free space
(a) If the magnetic field at the centre of the coil is considered, then x = 0.
∴ B = `(μ_0"IR"^2"N")/(2"R"^3) = (μ_0"IN")/(2"R")`
This is the familiar result for magnetic field at the centre of the coil.
(b) Radii of two parallel co-axial circular coils = R
Number of turns on each coil = N
Current in both coils = I
Distance between both the coils = R
Let us consider point Q at distance d from the centre.
Then, one coil is at a distance of `"R"/2 + "d"` from point Q.
∴ Magnetic field at point Q is given as:
B1 = `(μ_0"NIR"^2)/(2[("R"/2 + "d")^2 + "R"^2]^(3/2))`
Also, the other coil is at a distance of `"R"/2 - "d"` from point Q.
∴ Magnetic field due to this coil is given as:
B2 = `(μ_0"NIR"^2)/(2[("R"/2 - "d")^2 + "R"^2]^(3/2))`
Total magnetic field,
B = B1 + B2
= `(μ_0"IR"^2)/2 [{("R"/2 - "d")^2 + "R"^2}^(3/2) + {("R"/2 + "d")^2 + "R"^2}^(3/2)]`
= `(μ_0"IR"^2)/2 [((5"R"^2)/4 + "d"^2 - "Rd")^(3/2) + ((5"R"^2)/4 + "d"^2 + "Rd")^(3/2)]`
= `(μ_0"IR"^2)/2 xx ((5"R"^2)/4)^(3/2) [(1 + 4/5 "d"^2/"R"^2 - 4/5 "d"/"R")^{3/2) + (1 + 4/5 "d"^2/"R"^2 + 4/5 "d"/"R")^(3/2)]`
For d << R, neglacting the factor `"d"^2/"R"^2`, we get:
`≈ (μ_0"IR"^2)/2 xx ((5"R"^2)/4)^(3/2) xx [(1 - (4"d")/(5"R"))^(3/2) + (1 + (4"d")/(5"R"))^(3/2)]`
`≈ (μ_0"IR"^2"N")/(2"R"^3) xx (4/5)^(3/2) [1 - (6"d")/(5"R") + 1 + (6"d")/(5"R")]`
B = `(4/5)^(3/2) (μ_0"IN")/"R" = 0.72 ((μ_0"IN")/"R")`
Hence, it is proved that the field on the axis around the mid-point between the coils is uniform.
APPEARS IN
RELATED QUESTIONS
Seema’s uncle was advised by his doctor to have an MRI (Magnetic Resonance Imaging) scan of his brain. Her uncle felt it to be expensive and wanted to postpone it. When Seema learnt about this, she took the help of her family and also approached the doctor, who also offered a substantial discount. She then convinced her uncle to undergo the test to enable the doctor to know the condition of his brain. The information thus obtained greatly helped the doctor to treat him properly.
Based on the above paragraph, answer the following questions:
(a) What according to you are the values displayed by Seema, her family and the doctor?
(b) What could be the possible reason for MRI test to be so expensive?
(c) Assuming that MRI test was performed using a magnetic field of 0.1 T, find the minimum and maximum values of the force that the magnetic field could exert on a proton (charge = 1.6 x 10-19 C) moving with a speed of 104 m/s.
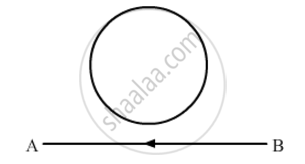
The electric current flowing in a wire in the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?
Magnetic lines of force always cross each other
An electron is moving with a speed of 3.2 × 107 m/s in a magnetic field of 6.00 × 10-4 T perpendicular to its path. What will be the radium of the path? What will be frequency and the energy in keV?
[Given: mass of electron = 9.1 × 10−31 kg, charge e = 1.6 × 10−19 C, 1 eV = 1.6 × 10−19 J]
The magnetic force depends on v which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that the net acceleration has a different value in different frames of reference?
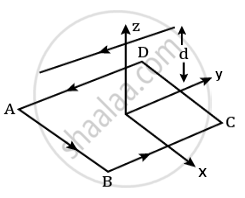
Figure shows a square loop. 20 cm on each side in the x-y plane with its centre at the origin. The loop carries a current of 7 A. Above it at y = 0, z = 12 cm is an infinitely long wire parallel to the x axis carrying a current of 10 A. The net force on the loop is ______ × 10-4 N.
Distinguish between the forces experienced by a moving charge in a uniform electric field and in a uniform magnetic field. (Any two points)
Lorentz force in vector form is ______.
