Advertisements
Advertisements
प्रश्न
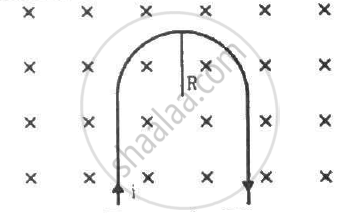
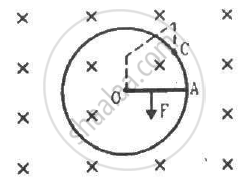
A rigid wire consists of a semi-circular portion of radius R and two straight sections (figure). The wire is partially immersed in a perpendicular magnetic field B, as shown in the figure. Find the magnetic force on the wire if it carries a current i.
उत्तर
Given:-
Radius of the semi-circular portion of the rigid wire = R
Magnetic field = B
Electric current flowing through the wire = i
As per the question, the wire is partially immersed in a perpendicular magnetic field.
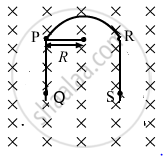
As PQ and RS are straight wires of length l each and strength of the magnetic field is also same on both the wires, the force acting on these wires will be equal in magnitude but their directions will be opposite to each other.(Direction of force can be found out using Fleming's left hand rule.)
So, the magnetic force on the wire PQ and the force on the wire RS are equal and opposite to each other. Both the forces cancel each other.
Therefore, only the semicircular loop PR will experience a net magnetic force.
Here, angle between the length of the wire and magnetic field, θ = 90˚
Magnetic force in the loop PR,
`vecF = iveclxxvecB`
Here, l = 2R
`vecF=i2R xx vecB`
`vecF = i2RB sin90^circ`
APPEARS IN
संबंधित प्रश्न
A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 30° to a uniform magnetic field. It experiences a torque of 0.063 J.
(i) Calculate the magnitude of the magnetic field.
(ii) In which orientation will the bar magnet be in stable equilibrium in the magnetic field?
Can a charged particle be accelerated by a magnetic field? Can its speed be increased?
A particle moves in a region with a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
A vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected
A wire of length l carries a current i long the x-axis. A magnetic field exists, which is given as `vecB = B_0 (veci + vecj + veck)` T. Find the magnitude of the magnetic force acting on the wire.
A current of 5.0 A exists in the circuit shown in the figure. The wire PQ has a length of 50 cm and the magnetic field in which it is immersed has a magnitude of 0.20 T. Find the magnetic force acting on the wire PQ.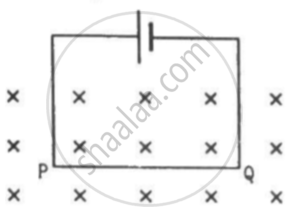
Consider a straight piece of length x of a wire carrying a current i. Let P be a point on the perpendicular bisector of the piece, situated at a distance d from its middle point. Show that for d >> x, the magnetic field at P varies as 1/d2 whereas for d << x, it varies as 1/d.
A long, straight wire is fixed horizontally and carries a current of 50.0 A. A second wire having linear mass density 1.0 × 10−4 kg m−1 is placed parallel to and directly above this wire at a separation of 5.0 mm. What current should this second wire carry such that the magnetic repulsion can balance its weight?
Consider the situation shown in the figure. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. Find the magnitude of this force when the rod makes an angle θ with the vertical.
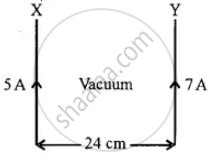
Two infinitely long current carrying conductors X and Y are kept parallel to each other, 24 cm apart in a vacuum. They carry currents of 5A and 7A respectively, in the same direction, as shown in the figure below. Find the position of a neutral point, i.e., a point where resultant magnetic flux density is zero. (Ignore earth’s magnetic field).
A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
(a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?
(b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before?
(Ignore the mass of the wires) g = 9.8 m s–2.
Correct expression for force on a current carrying conductor of length dl in a magnetic field is ______.
An electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
When a magnetic compass needle is carried nearby to a straight wire carrying current, then
- the straight wire cause a noticeable deflection in the compass needle.
- the alignment of the needle is tangential to an imaginary circle with straight wire as its centre and has a plane perpendicular to the wire.
A charged particle is moving on circular path with velocity v in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes ______.
A current of 3 A is flowing in a linear conductor having a length of 40 cm. The conductor is placed in a magnetic field of strength of 500 gauss and makes an angle of 30° with the direction of the field. It experiences a force of magnitude:
A conducting loop of resistance R and radius r has its centre at the origin of the coordinate system in a magnetic field of induction B. When it is rotated about y-axis through 90°, the net charge flown in the loop is directly proportional to: