Advertisements
Advertisements
प्रश्न
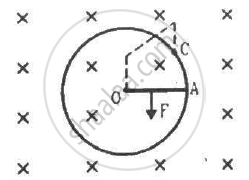
Consider the situation shown in the figure. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. Find the magnitude of this force when the rod makes an angle θ with the vertical.
उत्तर
When the circular loop is in the vertical plane, it tends to rotate in the clockwise direction because of its weight.
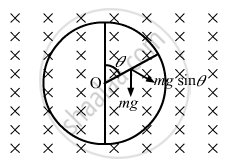
Let the force applied be F and its direction be perpendicular to the rod.
The component of mg along F is mg sin θ.
The magnetic force is in perpendicular and opposite direction to mg sin θ.
Now,
Current in the rod:-
\[i = \frac{B a^2 \omega}{2R}\]
The force on the rod is given by
\[F_B = iBl = \frac{B^2 a^2 \omega}{2R}\]
Net force \[= F −\frac{B^2 a^2 \omega}{2R}+mg \sin \theta\]
The net force passes through the centre of mass of the rod.
Net torque on the rod about the centre O:-
\[\tau = \left( F - \frac{B^2 a^3 \omega}{2R} + mg \sin\theta \right)\frac{OA}{2}\]
Because the rod rotates with a constant angular velocity, the net torque on it is zero.
i.e. τ = 0
\[\left( F - \frac{B^2 a^3 \omega}{2R} + mg \sin\theta \right)\frac{OA}{2} = 0\]
\[\therefore F = \frac{B^2 a^3 \omega}{2R} - mg \sin\theta\]
APPEARS IN
संबंधित प्रश्न
A small compass needle of magnetic moment ‘m’ is free to turn about an axis perpendicular to the direction of uniform magnetic field ‘B’. The moment of inertia of the needle about the axis is ‘I’. The needle is slightly disturbed from its stable position and then released. Prove that it executes simple harmonic motion. Hence deduce the expression for its time period.
A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 30° to a uniform magnetic field. It experiences a torque of 0.063 J.
(i) Calculate the magnitude of the magnetic field.
(ii) In which orientation will the bar magnet be in stable equilibrium in the magnetic field?
Can a charged particle be accelerated by a magnetic field? Can its speed be increased?
You are facing a circular wire carrying an electric current. The current is clockwise as seen by you. Is the field at the centre coming towards you or going away from you?
Two parallel wires carry currents of 20 A and 40 A in opposite directions. Another wire carying a current anti parallel to 20 A is placed midway between the two wires. T he magnetic force on it will be
A wire of length l carries a current i long the x-axis. A magnetic field exists, which is given as `vecB = B_0 (veci + vecj + veck)` T. Find the magnitude of the magnetic force acting on the wire.
Consider a solid sphere of radius r and mass m that has a charge q distributed uniformly over its volume. The sphere is rotated about its diameter with an angular speed ω. Show that the magnetic moment µ and the angular momentum l of the sphere are related as `mu = q/(2m) l`
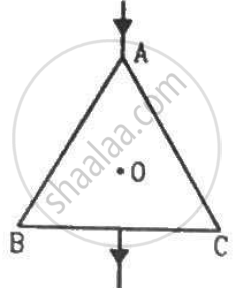
The wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.
A long wire carrying a current i is bent to form a place along α . Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
A long, straight wire is fixed horizontally and carries a current of 50.0 A. A second wire having linear mass density 1.0 × 10−4 kg m−1 is placed parallel to and directly above this wire at a separation of 5.0 mm. What current should this second wire carry such that the magnetic repulsion can balance its weight?
A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
(a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?
(b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before?
(Ignore the mass of the wires) g = 9.8 m s–2.
Correct expression for force on a current carrying conductor of length dl in a magnetic field is ______.
An electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
A charged particle is moving on circular path with velocity v in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes ______.
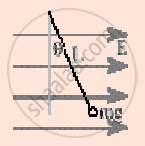
A small object with charge q and weight mg is attached to one end of a string of length ‘L’ attached to a stationary support. The system is placed in a uniform horizontal electric field ‘E’, as shown in the accompanying figure. In the presence of the field, the string makes a constant angle θ with the vertical. The sign and magnitude of q ______.
A conducting ring of radius 1m kept in a uniform magnetic field B of 0.01 T, rotates uniformly with an angular velocity 100 rad s−1 with its axis of rotation perpendicular to B. The maximum induced emf in it is:
A conducting loop of resistance R and radius r has its centre at the origin of the coordinate system in a magnetic field of induction B. When it is rotated about y-axis through 90°, the net charge flown in the loop is directly proportional to: