Advertisements
Advertisements
प्रश्न
A long wire carrying a current i is bent to form a place along α . Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
उत्तर
Let CAB be the wire making an angle α, P be the point on the bisector of this angle situated at a distance x from the vertex A and d be the perpendicular distance of AC and AB from P.
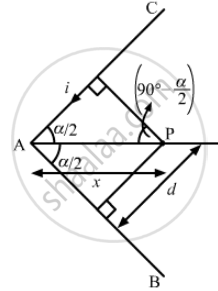
From the figure,
\[ = \frac{\mu_0 i}{4\pi x\sin \frac{\alpha}{2}}\left[ \sin \left( 90 - \frac{\alpha}{2} \right) + \sin 90 \right]\]
\[\frac{\mu_0 i}{4\pi x\sin \left( \frac{\alpha}{2} \right)}\left[ \cos \frac{\alpha}{2} + 1 \right]\]
\[ = \frac{\mu_0 i2 \cos^2 \left( \frac{\alpha}{4} \right)}{4\pi x2\sin \left( \frac{\alpha}{4} \right)\cos \left( \frac{\alpha}{4} \right)} = \frac{\mu_0 i\cot \left( \frac{\alpha}{4} \right)}{4\pi x}\]
Now, the magnetic field due to wires AC and AB is given by
APPEARS IN
संबंधित प्रश्न
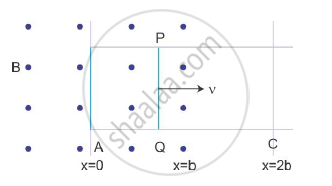
Sketch the change in flux, emf and force when a conducting rod PQ of resistance R and length l moves freely to and fro between A and C with speed v on a rectangular conductor placed in uniform magnetic field as shown in the figure
A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 30° to a uniform magnetic field. It experiences a torque of 0.063 J.
(i) Calculate the magnitude of the magnetic field.
(ii) In which orientation will the bar magnet be in stable equilibrium in the magnetic field?
Can a charged particle be accelerated by a magnetic field? Can its speed be increased?
A particle moves in a region with a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
A vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected
Two parallel wires carry currents of 20 A and 40 A in opposite directions. Another wire carying a current anti parallel to 20 A is placed midway between the two wires. T he magnetic force on it will be
A wire of length l carries a current i long the x-axis. A magnetic field exists, which is given as `vecB = B_0 (veci + vecj + veck)` T. Find the magnitude of the magnetic force acting on the wire.
A current of 5.0 A exists in the circuit shown in the figure. The wire PQ has a length of 50 cm and the magnetic field in which it is immersed has a magnitude of 0.20 T. Find the magnetic force acting on the wire PQ.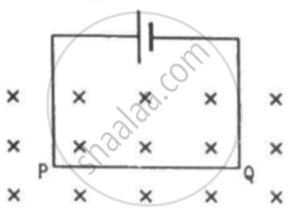
A rigid wire consists of a semi-circular portion of radius R and two straight sections (figure). The wire is partially immersed in a perpendicular magnetic field B, as shown in the figure. Find the magnetic force on the wire if it carries a current i.
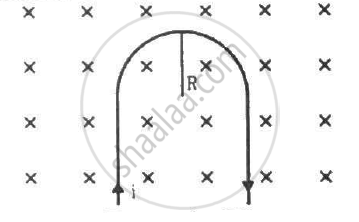
Figure shows a part of an electric circuit. The wires AB, CD and EF are long and have identical resistance. The separation between the neighbouring wires is 1.0 cm. The wires AE and BF have negligible resistance and the ammeter reads 30 A. Calculate the magnetic force per unit length of AB and CD.

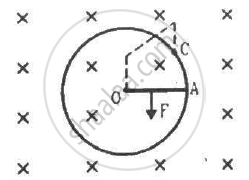
Consider the situation shown in the figure. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. Find the magnitude of this force when the rod makes an angle θ with the vertical.
An electron is projected with uniform velocity along the axis of a current carrying long solenoid. Which of the following is true?
When a magnetic compass needle is carried nearby to a straight wire carrying current, then
- the straight wire cause a noticeable deflection in the compass needle.
- the alignment of the needle is tangential to an imaginary circle with straight wire as its centre and has a plane perpendicular to the wire.
A charged particle is moving on circular path with velocity v in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes ______.
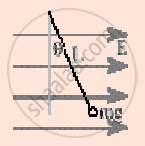
A small object with charge q and weight mg is attached to one end of a string of length ‘L’ attached to a stationary support. The system is placed in a uniform horizontal electric field ‘E’, as shown in the accompanying figure. In the presence of the field, the string makes a constant angle θ with the vertical. The sign and magnitude of q ______.
A conducting ring of radius 1m kept in a uniform magnetic field B of 0.01 T, rotates uniformly with an angular velocity 100 rad s−1 with its axis of rotation perpendicular to B. The maximum induced emf in it is:
