Advertisements
Advertisements
Question
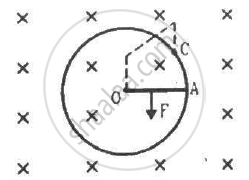
Consider the situation shown in the figure. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. Find the magnitude of this force when the rod makes an angle θ with the vertical.
Solution
When the circular loop is in the vertical plane, it tends to rotate in the clockwise direction because of its weight.
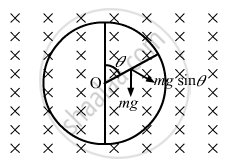
Let the force applied be F and its direction be perpendicular to the rod.
The component of mg along F is mg sin θ.
The magnetic force is in perpendicular and opposite direction to mg sin θ.
Now,
Current in the rod:-
\[i = \frac{B a^2 \omega}{2R}\]
The force on the rod is given by
\[F_B = iBl = \frac{B^2 a^2 \omega}{2R}\]
Net force \[= F −\frac{B^2 a^2 \omega}{2R}+mg \sin \theta\]
The net force passes through the centre of mass of the rod.
Net torque on the rod about the centre O:-
\[\tau = \left( F - \frac{B^2 a^3 \omega}{2R} + mg \sin\theta \right)\frac{OA}{2}\]
Because the rod rotates with a constant angular velocity, the net torque on it is zero.
i.e. τ = 0
\[\left( F - \frac{B^2 a^3 \omega}{2R} + mg \sin\theta \right)\frac{OA}{2} = 0\]
\[\therefore F = \frac{B^2 a^3 \omega}{2R} - mg \sin\theta\]
APPEARS IN
RELATED QUESTIONS
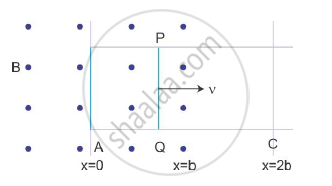
Sketch the change in flux, emf and force when a conducting rod PQ of resistance R and length l moves freely to and fro between A and C with speed v on a rectangular conductor placed in uniform magnetic field as shown in the figure
A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 30° to a uniform magnetic field. It experiences a torque of 0.063 J.
(i) Calculate the magnitude of the magnetic field.
(ii) In which orientation will the bar magnet be in stable equilibrium in the magnetic field?
Can a charged particle be accelerated by a magnetic field? Can its speed be increased?
Which of the following particles will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field?
A vertical wire carries a current in upward direction. An electron beam sent horizontally towards the wire will be deflected
Two parallel wires carry currents of 20 A and 40 A in opposite directions. Another wire carying a current anti parallel to 20 A is placed midway between the two wires. T he magnetic force on it will be
A wire of length l carries a current i long the x-axis. A magnetic field exists, which is given as `vecB = B_0 (veci + vecj + veck)` T. Find the magnitude of the magnetic force acting on the wire.
Consider a non-conducting plate of radius r and mass m that has a charge q distributed uniformly over it. The plate is rotated about its axis with an angular speed ω. Show that the magnetic moment µ and the angular momentum l of the plate are related as `mu = q/(2 m)l`
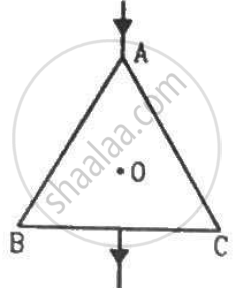
The wire ABC shown in figure forms an equilateral triangle. Find the magnetic field B at the centre O of the triangle assuming the wire to be uniform.
When a magnetic compass needle is carried nearby to a straight wire carrying current, then
- the straight wire cause a noticeable deflection in the compass needle.
- the alignment of the needle is tangential to an imaginary circle with straight wire as its centre and has a plane perpendicular to the wire.
A charged particle is moving on circular path with velocity v in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of magnetic field is halved, then radius becomes ______.
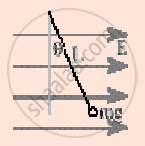
A small object with charge q and weight mg is attached to one end of a string of length ‘L’ attached to a stationary support. The system is placed in a uniform horizontal electric field ‘E’, as shown in the accompanying figure. In the presence of the field, the string makes a constant angle θ with the vertical. The sign and magnitude of q ______.
A current of 3 A is flowing in a linear conductor having a length of 40 cm. The conductor is placed in a magnetic field of strength of 500 gauss and makes an angle of 30° with the direction of the field. It experiences a force of magnitude:
A straight conductor of length 2m moves at a speed of 20 m/s. When the conductor makes an angle of 30° with the direction of magnetic field of induction of 0.1 wbm2 then induced emf:
A conducting ring of radius 1m kept in a uniform magnetic field B of 0.01 T, rotates uniformly with an angular velocity 100 rad s−1 with its axis of rotation perpendicular to B. The maximum induced emf in it is:
A conducting loop of resistance R and radius r has its centre at the origin of the coordinate system in a magnetic field of induction B. When it is rotated about y-axis through 90°, the net charge flown in the loop is directly proportional to: