Advertisements
Advertisements
प्रश्न
Derive an expression for the elastic energy stored per unit volume of a wire.
उत्तर
When a body is stretched, work is done against the restoring force (internal force). This work done is stored in the body in the form of elastic energy.
Consider a wire whose un-stretch length is L and the area of cross-section is A. Let a force produce an extension 1 and further assume that the elastic limit of the wire has not been exceeded and there is no loss in energy. Then, the work done by the force F is equal to the energy gained by the wire.
The work done in stretching the wire by dl, dW = Fdl
The total work done in stretching the wire from 0 to l is
W =
From Young’s modulus of elasticity,
Y =
Substituting equation (2) in equation (1), we get
W =
Since l is the dummy variable in the integration, we can change l to l’ (not in limits), therefore
W =
W =
Energy per unit volume is called energy density
u =
=
APPEARS IN
संबंधित प्रश्न
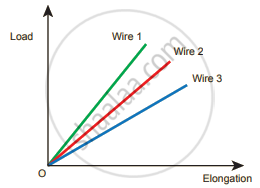
The load-elongation graph of three wires of the same material as shown in the figure. Which of the following wire is the thickest?
Two wires are made of the same material and have the same volume. The area of cross-sections of the first and the second wires are A and 2A respectively. If the length of the first wire is increased by ∆l on applying a force F, how much force is needed to stretch the second wire by the same amount?
The Young’s modulus for a perfect rigid body is __________.
Which of the following is not a scalar?
Define stress.
State Hooke’s law of elasticity
Define Poisson’s ratio.
What is the effect of temperature on elasticity?
Write down the expression for the elastic potential energy of a stretched wire.
A cylinder of length 1.5 m and diameter 4 cm is fixed at one end. A tangential force of 4 × 105 N is applied at the other end. If the rigidity modulus of the cylinder is 6 × 1010 Nm-2 then, calculate the twist produced in the cylinder.
