Advertisements
Advertisements
Question
Derive an expression for the elastic energy stored per unit volume of a wire.
Solution
When a body is stretched, work is done against the restoring force (internal force). This work done is stored in the body in the form of elastic energy.
Consider a wire whose un-stretch length is L and the area of cross-section is A. Let a force produce an extension 1 and further assume that the elastic limit of the wire has not been exceeded and there is no loss in energy. Then, the work done by the force F is equal to the energy gained by the wire.
The work done in stretching the wire by dl, dW = Fdl
The total work done in stretching the wire from 0 to l is
W = `int_0^"l" "Fdl"` .............(1)
From Young’s modulus of elasticity,
Y = `"F"/"A" xx "L"/"l"⇒ F = "YAl"/"L"` .........(2)
Substituting equation (2) in equation (1), we get
W = `int_0^"l" "YAl"/"L" "dl"`
Since l is the dummy variable in the integration, we can change l to l’ (not in limits), therefore
W = `int_0^"l" "YAl’"/"L" "dl’" = "YA"/"L"("l’"^2/2)_0^"l" = "YA"/"L" "l"^2/2 = 1/2 ("YAl"/"L")"l" = 1/2"Fl"`
W = `1/2` Fl = Elastic potential energy
Energy per unit volume is called energy density
u = `"Elastic potential energy"/"Volume" = (1/2 "Fl")/("AL")`
= `1/2 "F"/"A" "l"/"L" = 1/2 xx "Stress" xx "Strain"`
APPEARS IN
RELATED QUESTIONS
If a wire is stretched to double of its original length, then the strain in the wire is __________.
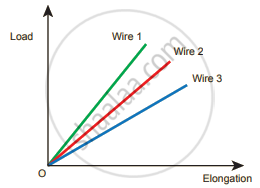
The load-elongation graph of three wires of the same material as shown in the figure. Which of the following wire is the thickest?
The following four wires are made of the same material. Which of these will have the largest extension when the same tension is applied?
Define strain.
State Hooke’s law of elasticity
Define Poisson’s ratio.
A spring balance shows wrong readings after using it for a long time. Why?
What is the effect of temperature on elasticity?
Explain the different types of modulus of elasticity.
Why the passengers are advised to remove the ink from their pens while going up in an aeroplane?
