Advertisements
Advertisements
Question
Explain the different types of modulus of elasticity.
Solution
From Hooke’s law, the stress in a body is proportional to the corresponding strain, provided the deformation is very small. Here we shall define the elastic modulus of a given material. There are three types of elastic modulus.
- Young’s modulus
- Rigidity modulus (or Shear modulus)
- Bulk modulus
Young’s Modulus: When a wire is stretched or compressed, then the ratio between tensile stress (or compressive stress) and tensile strain (or compressive strain) is defined as Young’s modules.
Young modulus of a material = `"Tensile stress or compressive stress"/"Tensile strain or compressive strain"`
Y = `σ_"t"/ε_"t"` or Y = `σ_"c"/ε_"c"`
S.I. unit of Young modulus is Nm−2 or pascal.
Bulk modulus: Bulk modulus is defined as the ratio of volume stress to the volume strain.
Bulk modulus, K = `"Normal (Perpendicular) stress or Pressure"/"Volume strain"`
The normal stress or pressure is σn = `"F"_"n"/(Δ"A") = Δ"P"`
The volume strain is εv = `(Δ"V")/"V"`
Therefore, Bulk modulus is K = `-(σ_"n")/(ε_"v") = -(Δ"P")/((Δ"V")/"V")`
The negative sign indicates when pressure is applied to the body, its volume decreases. Further, the equation implies that a material can be easily compressed if it has a small value of bulk modulus. In other words, bulk modulus measures the resistance of solids to change in their volume. For example, we know that gases can be easily compressed than solids, which means, gas has a small value of bulk modulus compared to solids. The S.I. unit of K is the same as that of pressure i.e., Nm–2 or Pa (pascal).
The rigidity modulus or shear modulus: The rigidity modulus is defined as the ratio of the shearing stress to shearing strain,
ηR = `"Shearing stress"/"Angle of shear or shearing strain"`
The shearing stress is σs = `"Tangential force"/"Area over which it is applied" = "F"_"t"/(Δ"A")`
The angle of shear or shearing strain εs = `"x"/"h"` = θ
Therefore, Rigidity modulus is ηR = `(σ_"s")/(ε_"s") = ("F"_"t"/(Δ"A"))/("x"/"h") = ("F"_"t"/(Δ"A"))/θ`
Further, the above implies, that a material can be easily twisted if it has a small value of rigidity modulus. For example, consider a wire, when it is twisted through an angle θ, a restoring torque is developed, that is
`τ ∝ θ`
This means that for a larger torque, the wire will twist by a larger amount (angle of shear θ is large). Since rigidity modulus is inversely proportional to the angle of shear, the modulus of rigidity is small. The S.I. unit of ηR is the same as that of pressure i.e., Nm–2 or pascal.
APPEARS IN
RELATED QUESTIONS
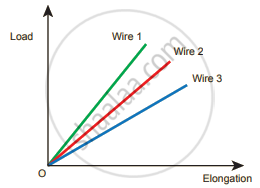
The load-elongation graph of three wires of the same material as shown in the figure. Which of the following wire is the thickest?
The Young’s modulus for a perfect rigid body is __________.
If the temperature of the wire is increased, then Young’s modulus will __________.
Copper of fixed volume V is drawn into a wire of length l. When this wire is subjected to a constant force F, the extension produced in the wire is ∆l. If Y represents Young’s modulus, then which of the following graphs is a straight line?
The following four wires are made of the same material. Which of these will have the largest extension when the same tension is applied?
Define strain.
Define Poisson’s ratio.
Derive an expression for the elastic energy stored per unit volume of a wire.
Why the passengers are advised to remove the ink from their pens while going up in an aeroplane?
We use the straw to suck soft drinks, why?
