Advertisements
Advertisements
Question
Derive an equation for the total pressure at a depth ‘h’ below the liquid surface.
Solution
In order to understand the increase in pressure with depth below the water surface, consider a water sample of cross-sectional area in the form of a cylinder. Let h1 and h2 be the depths from the air-water interface to level 1 and level 2 of the cylinder, respectively. Let F1 be the force acting downwards on level 1 and F2 be the force acting upwards on level 2, such that, F1 = P1 A and F2 = P2A. Let us assume the mass of the sample to be m and under equilibrium condition, the total upward force (F2) is balanced by the total downward force (F1 + mg), in other words, the gravitational force will act downward which is being exactly balanced by the difference between the force F2 – F1.
F2 – F1 = mg …… (1)
where m is the mass of the water available in the sample element. Let ρ be the density of the water then, the mass of water available in the sample element is
m = ρV = ρA (h2 – h1)
V = A (h2 – h1)
Hence, gravitational force, FG = ρA (h2 – h1) g
On substituting the W value in equation (1)
F2 = F1 + mg ⇒ P2A = P1A + ρA (h2 – h1) g
Cancelling out A on both sides,
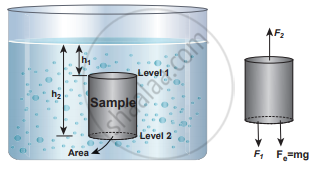
Sample of water with base area A in a static fluid with its forces in equilibrium
P2 = P1 + ρ(h2 – h1) g .........…(2)
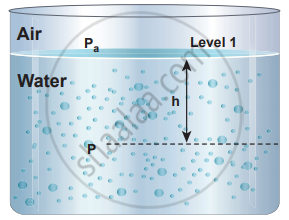
The pressure (P) at a depth (h) below the water surface
If we choose level 1 at the surface of the liquid (i.e., air-water interface) and level 2 at a depth ‘h’ below the surface, then the value of h1 becomes zero (h1 = 0) and in turn, P1 assumes the value of atmospheric pressure (say Pa). In addition, the pressure (P2) at a depth becomes P.
Substituting these values in the equation, we get
P = Pa + ρgh …… (3)
which means, the pressure at a depth h is greater than the pressure on the surface of the liquid, where Pa is the atmospheric pressure which is equal to 1.013 × 105 Pa.
If the atmospheric pressure is neglected or ignored then
P = ρgh ….. (4)
for a given liquid, ρ is fixed and g is also constant, then the pressure due to the fluid column is directly proportional to vertical distance or height of the fluid column. This implies the height of the fluid column is more important to decide the pressure and not the cross-sectional or base area or even the shape of the container.
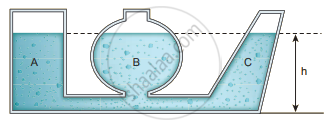
Illustration of hydrostatic parodox
Let us consider three vessels of different shapes A, B and C as shown in the figure. These vessels are connected at the bottom by a horizontal pipe. When they are filled with a liquid (say water), it occupies the same level even though the vessels hold different amounts of water. It is true because the liquid at the bottom of each section of the vessel experiences the same pressure.
APPEARS IN
RELATED QUESTIONS
State Pascal’s law in fluids.
State Archimedes principle.
What do you mean by upthrust or buoyancy?
State the law of floatation.
State and prove Pascal’s law in fluids.
State and prove Archimedes principle.
We can cut vegetables easily with a sharp knife as compared to a blunt knife. Why?
