Advertisements
Advertisements
प्रश्न
Derive the expression for centripetal acceleration.
उत्तर
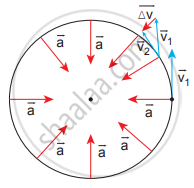
In a uniform circular motion, the velocity vector turns continuously without changing its magnitude (speed), as shown in the figure.

Velocity in a uniform circular motion
Note that the length of the velocity vector is not changed during the motion, implying that the speed remains constant. Even though the velocity is tangential at every point in the circle, the acceleration is acting towards the center of the circle. This is called centripetal acceleration. It always points towards the center of the circle. This is shown in the figure.
`(DeltavecV)/(Deltat) = veca`
Centripetal acceleration
The centripetal acceleration is derived from a simple geometrical relationship between position and velocity vectors.

The geometrical relationship between the position and velocity vectors
Let the directions of position and velocity vectors shift through the same angle θ in a small interval of time ∆t, as shown in the figure. For uniform circular motion, r = `|vecr_1|` = `|vecr_2|` and v = `|vecv_1|` = `|vecv_2|`. If the particle moves from position vector `vecr_1` to `vecr_2`, the displacement is given by `Deltavecr = vecr_2 - vecr_1`,. and the change in velocity from `vecv_1` to `vecv_2` is given by `∆vecv = vecv_2 – vecv_1`,. The magnitudes of the displacement ∆r and of ∆v satisfy the following relation. `(Δr)/r = (−Δv)/v = θ` Here the negative sign implies that ∆v points radially inward, towards the center of the circle.
`Deltav = -v((Deltar)/r)`
a = `(Deltav)/(Deltat) = v/r((Deltar)/(Deltat)) = -v^2/r`
For uniform circular motion v = cor, where co is the angular velocity of the particle about center. Then the centripetal acceleration can be written as.
a = -ω2r
APPEARS IN
संबंधित प्रश्न
An object is dropped in an unknown planet from a height of 50 m, it reaches the ground in 2 s. The acceleration due to gravity in this unknown planet is ______
Define velocity.
Define acceleration.
What is the difference between velocity and average velocity?
Define angular velocity.
Calculate the average velocity of the particle whose position vector changes from `vecr_1 = 5hati + 6hatj` to `vecr_2 = 2hati + 3hatj` in a time 5 second.
The following table gives the range of a particle when thrown on different planets. All the particles are thrown at the same angle with the horizontal and with the same initial speed. Arrange the planets in ascending order according to their acceleration due to gravity, (g value).
| Planet | Range |
| Jupiter | 50 m |
| Earth | 75 m |
| Mars | 90 m |
| Mercury | 95m |
The following graphs represent the velocity-time graph. Identify what kind of motion a particle undergoes in each graph.
| (a) | 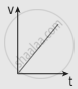 |
| (b) | 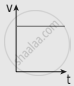 |
| (c) | 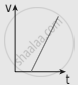 |
| (d) |  |
