Advertisements
Advertisements
प्रश्न
Derive the expression for total acceleration in the non-uniform circular motion.
उत्तर
If the speed of the object in circular motion is not constant, then we have non-uniform circular motion. For example, when the bob attached to a string moves in a vertical circle, the speed of the bob is not the same at all times. Whenever the speed is not the same in a circular motion, the particle will have both centripetal and tangential acceleration as shown in the figure.
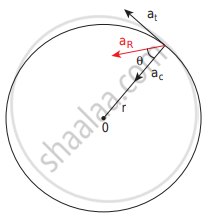
Resultant acceleration (aR) in a non-uniform circular motion
The resultant acceleration is obtained by the vector sum of centripetal and tangential acceleration Since centripetal acceleration is `v^2/r`, the magnitude of this resultant acceleration is given by `-a_R = sqrt(a_t^2 + (v^2/r)^2)`
This resultant acceleration makes an angle 0 with the radius vector as shown in the figure.
This angle is given by tan θ = `a_t/((v^2"/"r))`
APPEARS IN
संबंधित प्रश्न
A ball is projected vertically upwards with a velocity v. It comes back to the ground in time t. Which v-t graph shows the motion correctly?
A ball is dropped from some height towards the ground. Which one of the following represents the correct motion of the ball?
If a particle executes uniform circular motion, choose the correct statement.
What is non-uniform circular motion?
Write down the kinematic equations for angular motion.
Write down the expression for angle made by resultant acceleration and radius vector in the non-uniform circular motion.
Derive the kinematic equations of motion for constant acceleration.
Derive the equation of motion, range, and maximum height reached by the particle thrown at an oblique angle θ with respect to the horizontal direction.
The Moon is orbiting the Earth approximately once in 27 days, what is the angle transversed by the Moon per day?
A particle is projected at an angle of θ with respect to the horizontal direction. Match the following for the above motion.
(a) vx – decreases and increases
(b) vy – remains constant
(c) Acceleration – varies
(d) Position vector – remains downward
