Advertisements
Advertisements
Question
Derive the expression for total acceleration in the non-uniform circular motion.
Solution
If the speed of the object in circular motion is not constant, then we have non-uniform circular motion. For example, when the bob attached to a string moves in a vertical circle, the speed of the bob is not the same at all times. Whenever the speed is not the same in a circular motion, the particle will have both centripetal and tangential acceleration as shown in the figure.
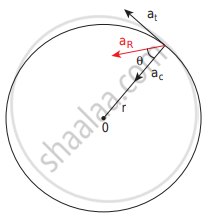
Resultant acceleration (aR) in a non-uniform circular motion
The resultant acceleration is obtained by the vector sum of centripetal and tangential acceleration Since centripetal acceleration is `v^2/r`, the magnitude of this resultant acceleration is given by `-a_R = sqrt(a_t^2 + (v^2/r)^2)`
This resultant acceleration makes an angle 0 with the radius vector as shown in the figure.
This angle is given by tan θ = `a_t/((v^2"/"r))`
APPEARS IN
RELATED QUESTIONS
A ball is projected vertically upwards with a velocity v. It comes back to the ground in time t. Which v-t graph shows the motion correctly?
A ball is dropped from some height towards the ground. Which one of the following represents the correct motion of the ball?
If a particle executes uniform circular motion, choose the correct statement.
Write down the kinematic equations for angular motion.
Write down the expression for angle made by resultant acceleration and radius vector in the non-uniform circular motion.
Derive the kinematic equations of motion for constant acceleration.
Derive the equations of motion for a particle (a) falling vertically (b) projected vertically.
Derive the equation of motion, range, and maximum height reached by the particle thrown at an oblique angle θ with respect to the horizontal direction.
The Moon is orbiting the Earth approximately once in 27 days, what is the angle transversed by the Moon per day?
A particle is projected at an angle of θ with respect to the horizontal direction. Match the following for the above motion.
(a) vx – decreases and increases
(b) vy – remains constant
(c) Acceleration – varies
(d) Position vector – remains downward
