Advertisements
Advertisements
प्रश्न
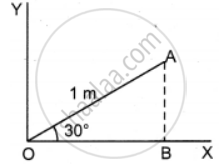
The position vector particle has a length of 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?
उत्तर
Given,
Length of position vector = 1 m
Angle made with x axis = 30
Solution:
Length of X component (OB) = OA cos θ
= 1 × cos 30°
= `sqrt3/2` (or) 0.87 m
Length of Y component (AB) = OA sin θ = 1 × sin 30°
= `1/2` = 0.5 m.
APPEARS IN
संबंधित प्रश्न
If `veca=4hati-hatj+hatk` then find a unit vector parallel to the vector `veca+vecb`
How do you deduce that two vectors are perpendicular?
If the horizontal and vertical components of a force are negative, then that force is acting in between
If a line makes angles 120° and 60° with the positive directions of X and Z axes respectively then the angle made by the line with positive Y-axis is ______.
If `veca = 4hati + 6hatj` and `vecb = 3hatj + 4hatk`, then the vector form of the component of `veca` along `vecb` is ______.
If `4hati - 5hatj + hatk, 2hati + 3hatj + 3hatk` and `xhati + yhatj + zhatk` represent the sides AB, BC and AC respectively of a triangle ABC, then find x, y, z.
Check whether the vectors `2hati + 2hatj +3hatk, -3hati +3hatj +2hatk` and `3hati +4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj+ 3hatk`, `-3hati + 3hatj +2hatk` and `3hati + 4hatk` form a triangle or not.
If `veca = 3hati - 2hatj + hatk` and `vecb = 2hati - 4hatj - 3hatk` then the value of `|veca - 2vecb|` will be ______.
Check whether the vectors `2hati + 2hatj + 3hatk , -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
