Advertisements
Advertisements
प्रश्न
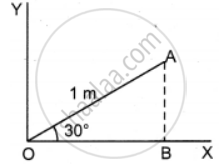
The position vector particle has a length of 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?
उत्तर
Given,
Length of position vector = 1 m
Angle made with x axis = 30
Solution:
Length of X component (OB) = OA cos θ
= 1 × cos 30°
= `sqrt3/2` (or) 0.87 m
Length of Y component (AB) = OA sin θ = 1 × sin 30°
= `1/2` = 0.5 m.
APPEARS IN
संबंधित प्रश्न
Write the number of vectors of unit length perpendicular to both the vectors `veca=2hati+hatj+2hatk and vecb=hatj+hatk`
Find a vector in the direction of vector `5hati - hatj +2hatk` which has a magnitude of 8 units.
If `overline(a),overline(b),overline(c)` are non-coplanar vectors and λ is a real number then `[lambda(overline(a)+overline(b))lambda^2overline(b) lambda overline(c)]=[overline(a) overline(b)+overline(c) overline(b)]` for ______.
If the horizontal and vertical components of a force are negative, then that force is acting in between
Find the vector component of the vector with initial point (2, 1) and terminal point (–5, 7).
Unit vector perpendicular to the plane of the triangle ABC with position vectors `veca, vecb, vecc` of the vertices A, B, C is ______.
If a line makes angles 120° and 60° with the positive directions of X and Z axes respectively then the angle made by the line with positive Y-axis is ______.
If `veca = 4hati + 6hatj` and `vecb = 3hatj + 4hatk`, then the vector form of the component of `veca` along `vecb` is ______.
If `4hati - 5hatj + hatk, 2hati + 3hatj + 3hatk` and `xhati + yhatj + zhatk` represent the sides AB, BC and AC respectively of a triangle ABC, then find x, y, z.
Check whether the vectors `2hati + 2hatj +3hatk, -3hati +3hatj +2hatk` and `3hati +4hatk` form a triangle or not.
