Advertisements
Advertisements
प्रश्न
Derive the expression for the force on a current-carrying conductor in a magnetic field.
उत्तर
- The force experienced is equal to the sum of Lorentz forces on the individual charge carriers in the wire.
- Consider a small length of wire ‘dl’, area – A, Current – I.
- The free electrons drift opposite to the direction of the current.
- The relation between I & Vd is given by
I = neAVd
- In magnetic field, the force experienced is given by
`vec"F" = - "e" (vec"v"_"d" xx vec"B")`
n → number of free electrons per unit volume.
n = `"N"/"V"`
V = A dl - Lorentz force = n A dl × – `"e"(vec"v"_"d" xx vec"B")`
dF = -enA dl `(vec"v"_"d" xx vec"B")` - Current element, `"I"vec"dl" = - "enA"vec"v"_"d"`
`therefore "d"vec"F" = ("l" vec"dl" = vec"B")`
`vec"F" = ("l" vec"l" xx vec"B")`
F = BIl sin θ
Case (i):
If the conductor is along the magnetic field; θ = 0° ; F = 0.
Case (ii):
If the conductor is perpendicular to the magnetic field; θ = 90°; F = BIl.
APPEARS IN
संबंधित प्रश्न
Define magnetic declination.
Define magnetic inclination.
A bar magnet having a magnetic moment `vec"M"` is cut into four pieces i.e., first cut in two pieces along the axis of the magnet and each piece is further cut into two pieces. Compute the magnetic moment of each piece.
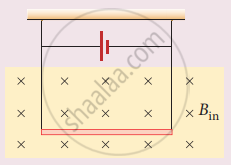
A conductor of linear mass density 0.2 g m1 suspended by two flexible wire as shown in figure. Suppose the tension in the supporting wires is zero when it is kept inside the magnetic field of I T whose direction is into the page. Compute the current inside the conductor and also the direction for the current. Assume g = 10 m s-2.
Calculate the magnetic field at the center of a square loop which carries a current of 1.5 A, length of each loop is 50 cm.
