Advertisements
Advertisements
प्रश्न
Derive the relation between surface tension and surface energy per unit area.
Derive the relation between surface energy & surface tension.
उत्तर १
Surface tension tries to decrease the surface area of a liquid. For increasing surface area, the work has to be done against the surface tension and it is stored in the surface molecules in the form of potential energy
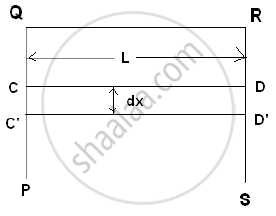
Consider a rectangular frame PQRS having a movable wire CD. Let QR = CD = L. If a soap film is formed on the frame CQRD, then the surface tension will try to pull the wire inward by a force F.
`"Surface tension" = "Force"/"free Length"`
F = Surface tension × Free length
∴ F = T × (2L)
If the wire is pulled out to C'D' through distance ‘dx’.
∴ Work done = F. dx
∴ W = T (2Ldx)
But increase in area = dA = 2Ldx
Surface energy is defined as the work done per unit area to increase the free surface area, under isothermal conditions.
`therefore "Surface energy"="Work done"/"Free surface area"=W/"dA"=(T(2Ldx))/(2Ldx)=T`
∴ Surface tension is also equal to the surface energy per unit area.
उत्तर २

Consider a C-shaped frame of wire P'PSS'. It is fitted with a movable arm QR, as shown in Fig. This frame is dipped in a soap solution and then taken out. A film of soap solution will be formed within the boundaries PQRS of the frame.
Each arm of the frame experiences an inward force due to the film. Under the action of this force, the movable arm QR moves towards side PS so as to decrease the area of the film. If the length of QR is L, then this inward force F acting on it is given by
F = (T) × (2L) ...(1)
Since the film has two surfaces, the upper surface and the lower surface, the total length over which surface tension acts on QR is 2L. Imagine an external force F' (equal and opposite to F) applied isothermally (gradually and at constant temperature) to the arm QR so that it pulls the arm away and tries to increase the surface area of the film. The arm QR moves to Q'R' through a distance dx. Therefore, the work done against F, the force due to surface tension, is given by
dw = F'dx
Using equation (1),
dw = T (2Ldx)
But, 2Ldx = dA, increase in area of the two surfaces of the film. Therefore, dw = T(dA).
This work done in stretching the film is stored in the area dA of the film as its potential energy. This energy is called surface energy.
∴ Surface energy = T (dA) ...(2)
Thus, surface tension is also equal to the surface energy per unit area.
APPEARS IN
संबंधित प्रश्न
Answer in one sentence.
State the SI unit and dimensions of stress.
The radius of a soap bubble is blown up to double its value under isothermal conditions. If 'r' be the initial radius of the bubble, and T be the surface tension, then energy spent in doubling the radius is ______
Assertion: If work done in increasing the size of a soap film from 10 cm x 4 cm to 10 cm x 8 cm is 2 x 10-4 J, then the surface tension is 5 x 10-4 N m-1.
Reason: Work done = Surface tension x increase in area.
If two identical mercury drops are combined to form a single drop, then its temperature will ____________.
Soap solution bubble having radius `1/sqrtπ` cm is expanded to a bubble of radius `4/sqrtπ`. If the surface tension of soap solution is 30 dyne/cm, then the work done is ______.
Which one of the following statements is correct?
Two spherical soap bubbles of radii r1 and r2 in vacuum coalesce under isothermal conditions. The resulting bubble has a radius R such that ____________.
A liquid drop having surface energy 'E' is spread into 216 droplets of same size. The final surface energy of the droplets is ____________.
If a million tiny droplets of water of the same radius coalesce into one larger drop, then the ratio of the surface energy of the large drop to the total surface energy of all the droplets will be ____________.
On the surface of the liquid in equilibrium, molecules of the liquid possess ____________.
Consider a process shown in the figure. During this process, the work done by the system ______.
A fix number of spherical drops of a liquid of radius 'r' coalesce to form a large drop of radius 'R' and volume 'V'. If 'T' is the surface tension then energy ______.
A water film is formed between the two straight parallel wires, each of length 10 cm, kept at a separation of 0.5 cm. Now, the separation between them is increased by 1 mm without breaking the water film. The work done for this is ______.
(surface tension of water = 7.2 x 10-2Nm-1)
A metal coin of thickness 'd' and density 'ρ' is floating on water of surface tension 'T'. The radius of the coin is ______.
g = acceleration due to gravity
One thousand small water drops of equal radii combine to form a big drop. The ratio of final surface energy to the total initial surface energy is ______.
The surface tension of a liquid is 10 N/m. If a thin film of the area 0.05 m2 is formed on a loop. Then the surface energy will be:
One cubic plate, having a 15 cm side, floats on water surface. If surface tension of water is 60 dyne/cm. To lift this plate from water, Find the extra force required against weight.
Calculate the work done in blowing a soap bubble to a radius of 1 cm. The surface tension of soap solution is 2.5 × 10-2 N/m.
If T1, T2 and T3 are the forces due to surface tension at the liquid-s solid-gas and liquid-gas interfaces such that T2 - T1 ≅ T3 and the contact angle for the liquid-solid pair is θ then ______.
Prove that, equivalent S.I. unit of surface tension is J/m2.
Calculate the amount of energy evolved when 343 droplets of mercury each of radius. 0.05 mm, combine to form one drop. The surface tension of mercury is 50 x 10-2 N/m.
