Advertisements
Advertisements
प्रश्न
Derive the relationship between density of substance, its molar mass, and the unit cell edge length. Explain how you will calculate the number of particles, and a number of unit cells in x g of metal.
Advertisements
उत्तर
- Relationship between density of a substance, its molar mass and the unit cell edge length:
- If edge length of cubic unit cell is ‘a’, then the volume of unit cell is a3.
- Suppose that mass of one particle is ‘m’ and that there are ‘n’ particles per unit cell.
∴ Mass of unit cell = m × n .....(1) - The density of unit cell (ρ), which is same as density of the substance is given by:
`rho = "Mass of unit cell"/"Volume of a unit cell"`
= `("m" xx "n")/"a"^3` = Density of substance …(2) - Molar mass (M) of the substance is given by:
M = mass of one particle × number of particles per mole
= m × NA (NA is Avogadro number)
Therefore, m = `"M"/"N"_"A"` .....(3) - Combining equations (2) and (3), gives
`rho = ("n M")/("a"^3 "N"_"A")` .....(4)
- The density (ρ) and molar mass (M) of metal are related to each other through unit cell parameters as given below:
`rho = "n"/"a"^3 xx "M"/"N"_"A"`
∴ M = ρ`("a"^3 "N"_"A")/"n"`
where, ‘n’ is the number of particles in unit cell and ‘a3’ is the volume of unit cell.
- The number of particles in x g of metallic crystal:
∴ Molar mass, M, contains NA particles.
∴ x g of metal contains `(x"N"_"A")/"M"` particles.
Substitution of M in the above equation gives
Number of particles in ‘x’ g = `(x"N"_"A")/(rho"a"^3"N"_"A"//"n") = "x n"/(rho "a"^3)` - Number of unit cells in x g of metallic crystal:
‘n’ particles correspond to 1 unit cell.
∴ `(x"n")/(rho"a"^3)` particles correspond to `(x"n")/(rho"a"^3) xx 1/"n"` unit cells.
∴ Number of unit cells in ‘x’ g metal = `x/(rho"a"^3)`
संबंधित प्रश्न
An element with molar mass 27 g/mol forms a cubic unit cell with edge length of 405 p.m. If the density of the element is 2.7 g/cm3, what is the nature of the cubic unit cell?
Give the percentage of empty space in bcc lattice.
If the total volume of a simple cubic unit cell is 6.817 × 10-23 cm3, what is the volume occupied by particles in the unit cell?
Calculate the number of unit cells in 0.3 g of a species having density of 8.5 g/cm3 and unit cell edge length 3.25 × 10-8 cm.
The pyranose structure of glucose is ____________.
Silver crystallises in fcc structure, if edge length of unit cell is 316.5 pm. What is the radius of silver atom?
An element crystallizes in fcc type of unit cell. The volume of one unit cell is 24.99 × 10-24 cm3 and density of the element 7.2 g cm-3, Calculate the number of unit cells in 36 g of pure sample of element?
What is the percentage of unoccupied space in fcc unit cell?
In bcc unit cell, the edge length (a) and radius of sphere (r) are related to each other by equation:
An element (atomic mass M g/mol) having bcc structure has unit cell edge 400 pm. The density of the element is ____________ g/cm3.
[NA = 6.0 × 1023 atom mol−1)
How many total constituent particles are present in simple cubic unit cell?
The percentage of unoccupied volume in simple cubic cell is ______.
If the edge of a body-centred unit cell is 360 pm, what will be the approximate radius of the atom present in it? (in pm)
An element crystallizes bcc type of unit cell, the density and edge length of unit cell is 4 g cm−3 and 500 pm respectively. What is the atomic mass of an element?
Consider the following unit cell.
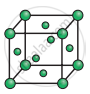
The number of particles (spheres) per unit cell is:
A metallic element has a cubic lattice with edge length of unit cell 2 Å. Calculate the number of unit cells in 200 g of the metal, if density of metal is 2.5 g cm-3?
What is the density of iron crystal which crystallizes in body-centred cubic structure with edge length 287 pm? (At. mass of Fe = 56 amu)
The number of atoms in 100 g of an fcc crystal with density 10 g cm-3 and unit cell edge length 200 pm is equal to ______.
The coordination number of atoms in body-centred cubic structure (bcc) is ______.
Calculate the density of metal with molar mass 56 g mol- 1 that crystallises to form a bcc structure with edge length 288 pm.
An element with molar mass 2.7 × 10-2 kg/mol. Forms a cubic units cell with edge length of 405 pm. If the density is 2.7 × 103 kg/m3. Find the nature of a cubic unit cell.
The correct sequence of the atomic layers in cubic close packing is ______.
The total number of different primitive unit cells is ______.
What would be the empirical formula of a compound having a unit cell containing A ion shared equally at the corner of the cube and B ion on the centre of faces of the cube?
The number of particles present in Face Centred Cubic Unit cell is/are ______.
