Advertisements
Advertisements
प्रश्न
Determine the maximum angular speed of an electron moving in a stable orbit around the nucleus of the hydrogen atom.
उत्तर
The radius of the nth Bohr orbit is
r = `(ε_0"h"^2"n"^2)/(pi"mZe"^2)` ....(1)
and the linear speed of an electron in this orbit is
v = `"Ze"^2/(2ε_0"nh")` ....(2)
where ε0 ≡ permittivity of free space, h =Planck's constant, n ≡ principal quantum number, m ≡ electron mass, e ≡ electronic charge and Z = the atomic number of the atom.
Since angular speed ω = `"v"/"r"`, then from Eqs. (1) and (2), we get,
ω = `"v"/"r" = "Ze"^2/(2ε_0"nh") * (pi"mZe"^2)/(ε_0"h"^2"n"^2) = (pi"mZ"^2"e"^4)/(2ε_0^2"h"^3"n"^3)` ...(3)
which gives the required expression for the angular speed of an electron in the nth Bohr orbit. From Eq. (3), the frequency of revolution of the electron,
f = `omega/(2pi) = 1/(2pi) xx (pi"mZ"^2"e"^4)/(2ε_0^2"h"^3"n"^3) = ("mZ"^2"e"^4)/(4ε_0^2"h"^3"n"^3)` .....(4)
Obtain the formula for w and continue as follows:
ω(maximum) = `(pi"me"^4)/(2ε_0^2"h"^3)` (for Z = 1 and n = 1)
`= ((3.142)(9.1 xx 10^-31 "kg")(1.6 xx 10^-19"C")^4)/((2)(8.85 xx 10^-12"C"^2//"N.m"^2)^2(6.63 xx 10^-34 "J.s")^3)` rad/s
`= ((3.142)(9.1)(1.6)^4(10^-107))/((2)(8.85)^2(6.63)^3(10^-126))`
= 4.105 × 1016 rad/s
APPEARS IN
संबंधित प्रश्न
What is the difference between a nuclear reactor and a nuclear bomb?
The half-life of \[\ce{_38^90Sr}\] is 28 years. Determine the disintegration rate of its 5 mg sample.
The mass of the earth is 81 times the mass of the moon and the distance between their centres is R. The distance from the centre of the earth, where gravitational force will be zero is ______.
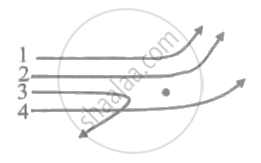
The diagram shows the path of four `alpha` - particles of the same energy being scattered by the nucleus of an atom simultaneously. Which of these are/is not physically possible?
Two protons are kept at a separation of 10 nm. Let Fn and Fe be the nuclear force and the electromagnetic force between them ____________.
The radius of germanium (Ge) nuclide is measured to be twice the radius of `""^9""_4"Be"`. The number of nucleons in Ge will be ____________.
If radius of the `{:(27),(13):}` Al nucleus is taken to be RAI then the radius of `{:(125), (53):}` Te nucleus is ____________.
A sample of radioactive element contains 8 × 1016 active nuclei. The half-life of the element is 15 days. The number of nuclei decayed after 60 days is ______.
Explain how nuclear size of an atom is estimated.
Define the term Nucleons.
