Advertisements
Advertisements
प्रश्न
Determine whether the following statement is true or false. Justify your answer.
For all sets A, B, and C, A – (B – C) = (A – B) – C
विकल्प
True
False
उत्तर
This statement is False.
Explanation:

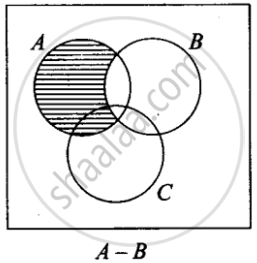
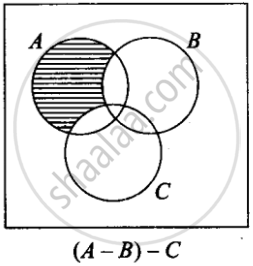
From the Venn Diagrams
A – (B – C) ≠ (A – B) – C
APPEARS IN
संबंधित प्रश्न
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
5 _____ A
List all the elements of the following set:
D = {x : x is a letter in the word “LOYAL”}
Which of the following collection are sets? Justify your answer:
The collection of all girls in your class.
Which of the following collection are sets? Justify your answer:
The collection of prime integers.
If A = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], then insert the appropriate symbol ∈ or ∉ in each of the following blank space:
9 ...... A
Describe the following sets in Roster form:
{x ∈ N : x2 < 25};
Describe the following sets in Roster form:
{x ∈ N : x = 2n, n ∈ N};
Describe the following sets in Roster form:
The set of all letters in the word 'Better'.
Describe the following sets in set-builder form:
B={1,1/2 ,1/3, 1/4,1/5,...........};
Describe the following sets in set-builder form:
E = {0}
Describe the following sets in set-builder form:
{5, 25, 125 625}
List all the elements of the following sets:
\[A = \left\{ x: x^2 \leq 10, x \in Z \right\}\]
Write the set of all vowels in the English alphabet which precede q.
Write the set \[\left\{ \frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50} \right\}\] in the set-builder form.
Which of the following statements are correct?
Write a correct form of each of the incorrect statement.
\[a \in {\left\{ a \right\}, b}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ \left\{ c, d \right\} \right\} \subset A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[1 \in A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\phi \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[2 \subset A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true?\[\left\{ \left\{ \phi \right\} \right\} \subset A\]
Write down all possible proper subsets each of the following set:
{1, 2},
If A is any set, prove that: \[A \subseteq \phi \Leftrightarrow A = \phi .\]
Describe the following set in Set-Builder form
{0, –1, 2, –3, 4, –5, 6, ...}
There are 260 persons with skin disorders. If 150 had been exposed to chemical A, 74 to chemical B, and 36 to both chemicals A and B, find the number of persons exposed to Chemical A but not Chemical B
Write the following sets in the roaster form:
D = {t | t3 = t, t ∈ R}
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in English and Mathematics but not in Science.
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English and Sanskrit but not French
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study at least one of the three languages
State True or False for the following statement.
Given A = {0, 1, 2}, B = {x ∈ R | 0 ≤ x ≤ 2}. Then A = B.
