Advertisements
Advertisements
प्रश्न
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English and Sanskrit but not French
Advertisements
उत्तर
Let us use Venn diagram method.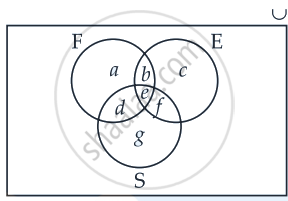
Total number of students = 50
⇒ n(U) = 50
Number of students who study French = 17
⇒ n(F) = 17
Number of students who study English = 13
⇒ n(E) = 13
Number of students who study Sanskrit = 15
⇒ n(S) = 15
Number of students who study French and English = 9
⇒ n(F ∩ E) = 9
Number of students who study English and Sanskrit = 4
⇒ n(E ∩ S) = 4
Number of students who study French and Sanskrit = 5
⇒ n(F ∩ S) = 5
Number of students who study French, English and Sanskrit = 3
⇒ n(F ∩ E ∩ S) = 3
n(F) = 17
a + b + d + e = 17 ......(i)
n(E) = 13
b + c + e + f = 13 ......(ii)
n(S) = 15
d + e + f + g = 15 ......(iii)
n(F ∩ E) = 9
∴ b + e = 9 ......(iv)
n(E ∩ S) = 4
∴ e + f = 4 .......(v)
n(F ∩ S) = 5
∴ d + e = 5 ......(vi)
n(E ∩ F ∩ S) = 3
∴ e = 3 .......(vii)
From (iv)
b + 3 = 9
⇒ b = 9 – 3 = 6
From (v)
3 + f = 4
⇒ f = 4 – 3 = 1
From (vi)
d + 3 = 5
⇒ d = 5 – 3 = 2
Now from equation (i)
a + 6 + 2 + 3 = 17
⇒ a = 17 – 11
⇒ a = 6
Now from equation (ii)
6 + c + 3 + 1 = 13
⇒ c = 13 – 10
⇒ c = 3
From equation (iii)
2 + 3 + 1 + g = 15
⇒ g = 15 – 6
⇒ g = 9
Number of students who study English and Sanskrit but not French, f = 1
APPEARS IN
संबंधित प्रश्न
Identify whether the following is set or not? Justify your answer.
The collection of all months of a year beginning with the letter J.
Identify whether the following is set or not? Justify your answer.
A team of eleven best-cricket batsmen of the world.
Identify whether the following is set or not? Justify your answer.
The collection of questions in this Chapter.
Write the following set in roster form:
B = {x : x is a natural number less than 6}
Write the following set in the set-builder form:
{3, 6, 9, 12}
List all the elements of the following set:
A = {x : x is an odd natural number}
List all the elements of the following set:
D = {x : x is a letter in the word “LOYAL”}
Match each of the set on the left in the roster form with the same set on the right described in set-builder form:
| (i) | {1, 2, 3, 6} | (a) | {x : x is a prime number and a divisor of 6} |
| (ii) | {2, 3} | (b) | {x : x is an odd natural number less than 10} |
| (iii) | {M, A, T, H, E, I, C, S} | (c) | {x : x is natural number and divisor of 6} |
| (iv) | {1, 3, 5, 7, 9} | (d) | {x : x is a letter of the word MATHEMATICS} |
Describe the following sets in Roster form:
{x : x is a letter before e in the English alphabet}
Describe the following sets in Roster form:
{x ∈ N : x2 < 25};
Describe the following sets in Roster form:
The set of all letters in the word 'Better'.
Describe the following sets in set-builder form:
E = {0}
Describe the following sets in set-builder form:
{5, 25, 125 625}
Write the set of all vowels in the English alphabet which precede q.
Write the set \[\left\{ \frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50} \right\}\] in the set-builder form.
Which of the following statement are correct?
Write a correct form of each of the incorrect statements.
\[a \subset \left\{ a, b, c \right\}\]
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\phi \subset \left\{ a, b, c \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ c, d \right\} \subset A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ \left\{ c, d \right\} \right\} \subset A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[a \in A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\phi \in A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\left\{ 6, 7, 8 \right\} \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[\left\{ 1 \right\} \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[2 \subset A\]
What is the total number of proper subsets of a set consisting of n elements?
Prove that:
\[A \subseteq B, B \subseteq C \text{ and } C \subseteq A \Rightarrow A = C .\]
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that \[\left( A \cap B \right)' = A' \cup B'\]
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read neither Marathi and English newspaper
Write the following interval in Set-Builder form.
(2, 5]
Answer the following:
In a school there are 20 teachers who teach Mathematics or Physics. Of these, 12 teach Mathematics and 4 teach both Physics and Mathematics. How many teachers teach Physics?
Given that E = {2, 4, 6, 8, 10}. If n represents any member of E, then, write the following sets containing all numbers represented by n + 1
Let X = {1, 2, 3, 4, 5, 6}. If n represent any member of X, express the following as sets:
n is greater than 4
Write the following sets in the roaster form:
D = {t | t3 = t, t ∈ R}
If Y = {x | x is a positive factor of the number 2p – 1 (2p – 1), where 2p – 1 is a prime number}.Write Y in the roaster form.
128 ∈ {y | the sum of all the positive factors of y is 2y}
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in Mathematics only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French only
If sets A and B are defined as A = `{(x, y) | y = 1/x, 0 ≠ x ∈ "R"}` B = {(x, y) | y = – x, x ∈ R}, then ______.
State True or False for the following statement.
Let sets R and T be defined as
R = {x ∈ Z | x is divisible by 2}
T = {x ∈ Z | x is divisible by 6}. Then T ⊂ R
