Advertisements
Advertisements
प्रश्न
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study Sanskrit only
उत्तर
Let us use Venn diagram method.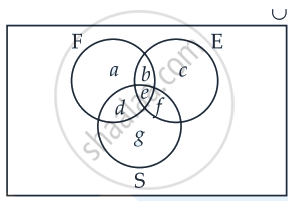
Total number of students = 50
⇒ n(U) = 50
Number of students who study French = 17
⇒ n(F) = 17
Number of students who study English = 13
⇒ n(E) = 13
Number of students who study Sanskrit = 15
⇒ n(S) = 15
Number of students who study French and English = 9
⇒ n(F ∩ E) = 9
Number of students who study English and Sanskrit = 4
⇒ n(E ∩ S) = 4
Number of students who study French and Sanskrit = 5
⇒ n(F ∩ S) = 5
Number of students who study French, English and Sanskrit = 3
⇒ n(F ∩ E ∩ S) = 3
n(F) = 17
a + b + d + e = 17 ......(i)
n(E) = 13
b + c + e + f = 13 ......(ii)
n(S) = 15
d + e + f + g = 15 ......(iii)
n(F ∩ E) = 9
∴ b + e = 9 ......(iv)
n(E ∩ S) = 4
∴ e + f = 4 .......(v)
n(F ∩ S) = 5
∴ d + e = 5 ......(vi)
n(E ∩ F ∩ S) = 3
∴ e = 3 .......(vii)
From (iv)
b + 3 = 9
⇒ b = 9 – 3 = 6
From (v)
3 + f = 4
⇒ f = 4 – 3 = 1
From (vi)
d + 3 = 5
⇒ d = 5 – 3 = 2
Now from equation (i)
a + 6 + 2 + 3 = 17
⇒ a = 17 – 11
⇒ a = 6
Now from equation (ii)
6 + c + 3 + 1 = 13
⇒ c = 13 – 10
⇒ c = 3
From equation (iii)
2 + 3 + 1 + g = 15
⇒ g = 15 – 6
⇒ g = 9
Number of students who study Sanskrit only, g = 9
APPEARS IN
संबंधित प्रश्न
Identify whether the following is set or not? Justify your answer.
The collection of all even integers.
Write the following set in the set-builder form:
{2, 4, 6, …}
Match each of the set on the left in the roster form with the same set on the right described in set-builder form:
| (i) | {1, 2, 3, 6} | (a) | {x : x is a prime number and a divisor of 6} |
| (ii) | {2, 3} | (b) | {x : x is an odd natural number less than 10} |
| (iii) | {M, A, T, H, E, I, C, S} | (c) | {x : x is natural number and divisor of 6} |
| (iv) | {1, 3, 5, 7, 9} | (d) | {x : x is a letter of the word MATHEMATICS} |
Which of the following collection are sets? Justify your answer:
The collection of all girls in your class.
Describe the following sets in Roster form:
{x : x is a letter before e in the English alphabet}
Describe the following sets in set-builder form:
E = {0}
Describe the following sets in set-builder form:
{1, 4, 9, 16, ..., 100}
List all the elements of the following sets:
\[A = \left\{ x: x^2 \leq 10, x \in Z \right\}\]
List all the elements of the following set:
F = {x : x is a letter of the word "MISSISSIPPI"}
Match each of the sets on the left in the roster form with the same set on the right described in the set-builder form:
| (i) | {A, P, L, E} | (i) | x : x + 5 = 5, x ∈ Z |
| (ii) | {5, −5} | (ii) | {x : x is a prime natural number and a divisor of 10} |
| (iii) | {0} | (iii) | {x : x is a letter of the word "RAJASTHAN"} |
| (iv) | {1, 2, 5, 10,} | (iv) | {x: x is a natural number and divisor of 10} |
| (v) | {A, H, J, R, S, T, N} | (v) | x : x2 − 25 = 0 |
| (vi) | {2, 5} | (vi) | {x : x is a letter of the word "APPLE"} |
Write the set of all vowels in the English alphabet which precede q.
Which of the following statement are correct?
Write a correct form of each of the incorrect statements.
\[a \subset \left\{ a, b, c \right\}\]
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Write down all possible subsets of each of the following set:
{a}
What is the total number of proper subsets of a set consisting of n elements?
If A is any set, prove that: \[A \subseteq \phi \Leftrightarrow A = \phi .\]
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
8 ____ A
Write the following interval in Set-Builder form:
[6, 12]
Write the following interval in Set-Builder form
(2, 5]
Given that E = {2, 4, 6, 8, 10}. If n represents any member of E, then, write the following sets containing all numbers represented by n2
Let X = {1, 2, 3, 4, 5, 6}. If n represent any member of X, express the following as sets:
n + 5 = 8
Write the following sets in the roaster from:
B = {x | x2 = x, x ∈ R}
State which of the following statement is true and which is false. Justify your answer.
35 ∈ {x | x has exactly four positive factors}.
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in more than one subject only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English and Sanskrit but not French
Let S = {x | x is a positive multiple of 3 less than 100}
P = {x | x is a prime number less than 20}. Then n(S) + n(P) is ______.
State True or False for the following statement.
Let sets R and T be defined as
R = {x ∈ Z | x is divisible by 2}
T = {x ∈ Z | x is divisible by 6}. Then T ⊂ R
