Advertisements
Advertisements
प्रश्न
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English only
उत्तर
Let us use Venn diagram method.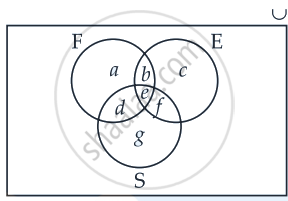
Total number of students = 50
⇒ n(U) = 50
Number of students who study French = 17
⇒ n(F) = 17
Number of students who study English = 13
⇒ n(E) = 13
Number of students who study Sanskrit = 15
⇒ n(S) = 15
Number of students who study French and English = 9
⇒ n(F ∩ E) = 9
Number of students who study English and Sanskrit = 4
⇒ n(E ∩ S) = 4
Number of students who study French and Sanskrit = 5
⇒ n(F ∩ S) = 5
Number of students who study French, English and Sanskrit = 3
⇒ n(F ∩ E ∩ S) = 3
n(F) = 17
a + b + d + e = 17 ......(i)
n(E) = 13
b + c + e + f = 13 ......(ii)
n(S) = 15
d + e + f + g = 15 ......(iii)
n(F ∩ E) = 9
∴ b + e = 9 ......(iv)
n(E ∩ S) = 4
∴ e + f = 4 .......(v)
n(F ∩ S) = 5
∴ d + e = 5 ......(vi)
n(E ∩ F ∩ S) = 3
∴ e = 3 .......(vii)
From (iv)
b + 3 = 9
⇒ b = 9 – 3 = 6
From (v)
3 + f = 4
⇒ f = 4 – 3 = 1
From (vi)
d + 3 = 5
⇒ d = 5 – 3 = 2
Now from equation (i)
a + 6 + 2 + 3 = 17
⇒ a = 17 – 11
⇒ a = 6
Now from equation (ii)
6 + c + 3 + 1 = 13
⇒ c = 13 – 10
⇒ c = 3
From equation (iii)
2 + 3 + 1 + g = 15
⇒ g = 15 – 6
⇒ g = 9
Number of students who study English only, c = 3
APPEARS IN
संबंधित प्रश्न
Write the following set in the set-builder form:
{2, 4, 8, 16, 32}
List all the elements of the following set:
B = `{x : x "is an integer", -1/2 < x < 9/2}`
List all the elements of the following set:
C = {x : x is an integer, x2 ≤ 4}
List all the elements of the following set:
D = {x : x is a letter in the word “LOYAL”}
List all the elements of the following set:
E = {x : x is a month of a year not having 31 days}
Which of the following collection are sets? Justify your answer:
The collection of all question in this chapter.
Describe the following sets in set-builder form:
D = {10, 11, 12, 13, 14, 15};
List all the elements of the following set:
\[B = \left\{ x: x = \frac{1}{2n - 1}, 1 \leq n \leq 5 \right\}\]
List all the elements of the following set:
F = {x : x is a letter of the word "MISSISSIPPI"}
Match each of the sets on the left in the roster form with the same set on the right described in the set-builder form:
| (i) | {A, P, L, E} | (i) | x : x + 5 = 5, x ∈ Z |
| (ii) | {5, −5} | (ii) | {x : x is a prime natural number and a divisor of 10} |
| (iii) | {0} | (iii) | {x : x is a letter of the word "RAJASTHAN"} |
| (iv) | {1, 2, 5, 10,} | (iv) | {x: x is a natural number and divisor of 10} |
| (v) | {A, H, J, R, S, T, N} | (v) | x : x2 − 25 = 0 |
| (vi) | {2, 5} | (vi) | {x : x is a letter of the word "APPLE"} |
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[a \in A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\left\{ 1, 2, 3 \right\} \subset A\]
Let\[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true?
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[\left\{ 1 \right\} \in A\]
Let \[\left\{ \left\{ 2 \right\}, \left\{ 1 \right\} \right\} \not\subset A\] Which of the following are true? \[\left\{ \left\{ 2 \right\}, \left\{ 1 \right\} \right\} \not\subset A\]
Write down all possible proper subsets each of the following set:
{1}.
Prove that:
\[A \subseteq B, B \subseteq C \text{ and } C \subseteq A \Rightarrow A = C .\]
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, = {2, 4, 6, 8} and C = {3, 4, 5, 6}.
Find \[\left( A \cap C \right)'\]
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take bot tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes at least one beverage, find the total number of students in the hostel.
Write the following interval in Set-Builder form
`(6, ∞)`
Write the following sets in the roaster form.
A = {x | x is a positive integer less than 10 and 2x – 1 is an odd number}
128 ∈ {y | the sum of all the positive factors of y is 2y}
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English and Sanskrit but not French
Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis. Then ______.
In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is ______.
If A and B are any two sets, then A – B is equal to ______.
State True or False for the following statement.
Given A = {0, 1, 2}, B = {x ∈ R | 0 ≤ x ≤ 2}. Then A = B.
