Advertisements
Advertisements
प्रश्न
दीर्घवृत्त `x^2/16 + y^2/9 = 1` से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
उत्तर
दिया गया दिर्घषवृतिय का समीकरण `x^2/16 + y^2/9 = 1`
दिया गए दीर्घवृत दोनों अक्ष के बारे में सममित है इसमे समरूप x और y समाहित हैं
`= y^2/9 = 1 - x^2/16`
`= y = pm 3/4 (sqrt(16 - x^2))`
दीर्घवृत द्वारा घिरा क्षेत्रफल = 4 (क्षेत्र का क्षेत्रफल) = 4 (क्षेत्रफल OAC)
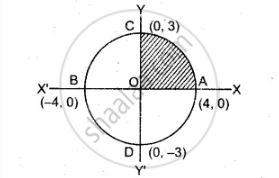
पहले चतुभुर्ज में दीर्घवृत `= 4 int_0^4 y dx = int_0^4 3/4 sqrt(16 - x^2) dx`
माना `x = 4 sin theta ; dx = 4 cos theta d theta`
अत: x = 0, `theta = 0 ;` जब x = 4, `theta = pi/2`
अपेक्षित क्षेत्र `= (4 xx 3)/4 int_0^(pi//2) sqrt(16 - 16 sin^2 theta). 4 cos theta d theta`
`= 3 int_0^(pi/2) 4sqrt(1 - sin^2 theta). 4 cos theta d theta`
`= 48 int_0^(pi/2) cos^2 theta d theta`
`= 24 int_0^(pi/2) (1 + cos 2 theta)d theta`
`= 24 [theta + (sin 2 theta)/2]_0^(pi/2)`
`= 12 pi` वर्ग इकाई
APPEARS IN
संबंधित प्रश्न
वक्र y2 = x रेखाओं x = 1, x = 4 एवं x-अक्ष से घिरे क्षेत्र का प्रथम पाद में क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थांश में वक्र y2 = 9x, x = 2, x = 4 एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थांश में x2 = 4y, y = 2, y = 4 एवं y-अंक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
दीर्घवृत्त `x^2/4 + y^2/9 = 1` से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
छेदक रेखा `x = a/sqrt2` द्वारा वृत्त x2 + y2 = a2 के छोटे भाग का क्षेत्रफल ज्ञात कीजिए।
परवलय y = x2 एवं y = |x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र x2 = 4y एवं रेखा x = 4y - 2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y2 = 4x एवं रेखा x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
प्रथम चतुर्थांश में वृत्त x2 + y2 = 4 एवं रेखाओं x = 0, x = 2 से घिरे क्षेत्र का क्षेत्रफल है:
वक्र y2 = 4x, y-अक्ष एवं रेखा y = 3 से घिरे क्षेत्र का क्षेत्रफल है:
दिए हुए वक्र एवं रेखा से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए:
y = x2; x = 1, x = 2 एवं x-अक्ष
दिए हुए वक्र एवं रेखा से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए:
y = x4; x = 1, x = 5 एवं x-अक्ष
प्रथम चतुर्थांश में सम्मिलित एवं y = 4x2, x = 0, y = 1 तथा y = 4 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय y = 4ax एवं रेखा y = mx से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय 4y = 3x2 एवं रेखा 2y = 3x + 12 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
दीर्घवृत्त `x^2/"a"^2 + "y"^2/"b"^2 = 1` एवं रेखा `x/"a" + "y"/"b" = 1` से घिरे लघु क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
परवलय x2 = y, रेखा y = x + 2 एवं x अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्रों {(x, y) : y ≥ x2 तथा y = |x|} से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
वक्र y = x|x|, x-अक्ष एवं कोटियों x = -1 तथा x = 1 से घिरे क्षेत्र का क्षेत्रफल है:
y-अक्ष, y = cosx एवं y = sin x, 0 ≤ x ≤ `pi/2` घिरे क्षेत्र का क्षेत्रफल है-
