Advertisements
Advertisements
प्रश्न
Divide. Write the quotient and the remainder.
(6x5 − 4x4 + 8x3 + 2x2) ÷ 2x2
उत्तर
(6x5 − 4x4 + 8x3 + 2x2) ÷ 2x2
= \[\frac{6 x^5 - 4 x^4 + 8 x^3 + 2 x^2}{2 x^2}\]
= \[\frac{2 x^2 \left( 3 x^3 - 2 x^2 + 4x + 1 \right)}{2 x^2}\]
= \[3 x^3 - 2 x^2 + 4x + 1\]
So, quotient = \[3 x^3 - 2 x^2 + 4x + 1\] and remainder = 0
संबंधित प्रश्न
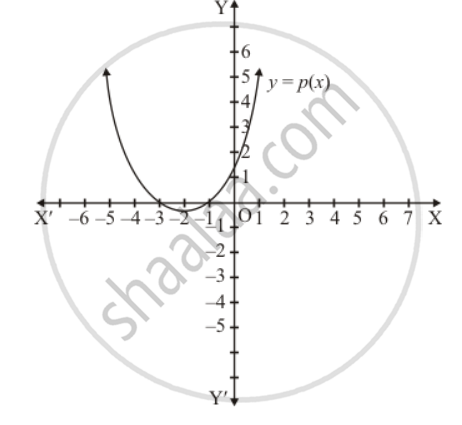
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
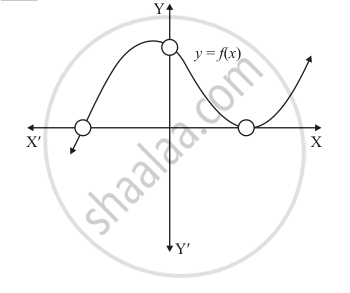
The graph of a polynomial y = f(x), shown in Fig. 2.18. Find the number of real zeros of f(x).
Give an example of polynomials f(x), g(x), q(x) and r(x) satisfying f(x) = g(x), q(x) + r(x), where degree r(x) = 0.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f(x)?
If graph of quadratic polynomial ax2 + bx + c cuts positive direction of y-axis, then what is the sign of c?
If α, β are the zeros of the polynomial p(x) = 4x2 + 3x + 7, then \[\frac{1}{\alpha} + \frac{1}{\beta}\] is equal to
If α, β are the zeros of the polynomial f(x) = x2 − p(x + 1) − c such that (α +1) (β + 1) = 0, then c =
Find the quadratic polynomial, sum, and product of whose zeroes are −1 and −20 respectively. Also, find the zeroes of the polynomial so obtained.
Determine the degree of the following polynomial:
–10
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the degree of the polynomial
