Advertisements
Advertisements
प्रश्न
दो चरों वाली रैखिक समीकरण 2x + 0y + 9 = 0 के किसी भी हल का रूप होता है
विकल्प
`(- 9/2, m)`
`(n, - 9/2)`
`(0, - 9/2)`
(– 9, 0)
उत्तर
`bb((- 9/2"," m))`
स्पष्टीकरण -
रैखिक समीकरण पर विचार करें -
2x + 0y + 9 = 0
अब, 2x = – 9
`x = - 9/2`
चूँकि, दिए गए समीकरण में y का गुणांक 0 है।
इसलिए, समाधान के रूप में दिया जा सकता है `(- 9/2, m)`।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित रैखिक समीकरण का दो चरों में आलेख खींचिए:- x + y = 4
निम्नलिखित रैखिक समीकरणों का दो चरों में आलेख खींचिए:- x - y = 2
नीचे दिए गए विकल्पों में से उस समीकरण को चुनिए जिसके आलेख दिए गए आंकड़ों में दिए गए हैं।
पहले आंकड़े के लिए
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

दूसरे आंकड़े के लिए
(i) y = x +2
(ii) y = x − 2
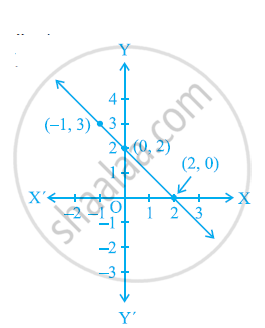
(iii) y = − x + 2
(iv) x + 2y = 6
अमरीका और कनाडा जैसे देशों में तापमान फारेनहाइट में मापा जाता है, जबकि भारत जैसे देशों में तापमान सेल्सियस में मापा जाता है। यहाँ फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण दिया गया है:
`F=(9/5)C+32`
-
सेल्सियस को x-अक्ष और फारेनहाइट को y-अक्ष मानकर ऊपर दिए गए रैखिक समीकरण का आलेख खींचिए।
-
यदि तापमान 30°C है, तो फारेनहाइट में तापमान क्या होगा?
-
यदि तापमान 95°F है, तो सेल्सियस में तापमान क्या होगा?
-
यदि तापमान 0°C है, तो फारेनहाइट में तापमान क्या होगा? और यदि तापमान 0°F है, तो
सेल्सियस में तापमान क्या होगा? -
क्या ऐसा भी कोई तापमान है जो फारेनहाइट और सेल्सियस दोनों के लिए संख्यात्मकत: समान है? यदि हाँ, तो उसे ज्ञात कीजिए।
रैखिक समीकरण 2x + 3y = 6 का आलेख y-अक्ष को निम्नलिखित में से किस बिंदु पर काटता है
x-अक्ष की समीकरण का रूप है
(a, a) रूप का बिंदु सदैव स्थित होता है
दो चरों वाली रैखिक समीकरण के आलेख का एक सरल रेखा होना आवश्यक नहीं है।
वह रैखिक समीकरण लिखिए, जिसके आलेख के प्रत्येक बिंदु की कोटि उसकी भुज की तीन गुनी है।
दर्शाइए कि बिंदु A(1, 2), B(– 1, – 16) और C(0, – 7) रैखिक समीकरण y = 9x – 7 के आलेख पर स्थित हैं।
