Advertisements
Advertisements
प्रश्न
Do you remember magic triangles? Come now, let s make some magic squares.
- Fill this square using all the numbers from 21 to 29.
Rule: The total of each side is 75.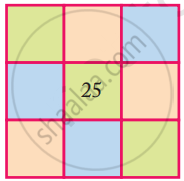
उत्तर
Given that total of each side is 75
We can use numbers from 21 to 29.
- In the first row:
The required number
= 75 – (26 + 22)
=75 – 48 = 27 - In the first column:
The required number
= 75 – (26 + 28)
= 75 – 54 = 21 - In the second row:
The required number
= 75 – (21 + 25)
= 75 = 75 – 46 = 29 - In the third row:
The required number
= 75 – (28 + 24)
= 75 – 52 = 23 - Number in first box = 28
Number in second box = 23
So, number in third box
= 75 – (28 + 23)
= 75 – 51= 24
Hence, the complete magic square is as follows:
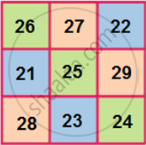
APPEARS IN
संबंधित प्रश्न
Which of the following statement is true?
The sum of two consecutive odd numbers is always divisible by 4.
Look at the patterns of numbers in hexagons.
Each side has 2 circles and 1 box.
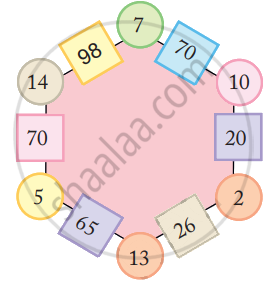
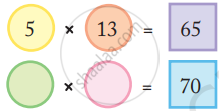
- Look at the number 65 in the box. Which are the circles next to it?
- Can you see how the rule works?
Use the same rule to fill the hexagons below.
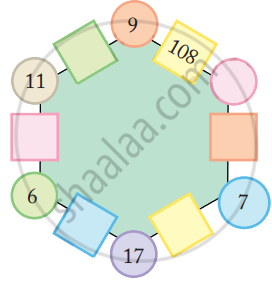
Now you also make your own magic hexagons.
Use the same rule to fill the hexagons below.
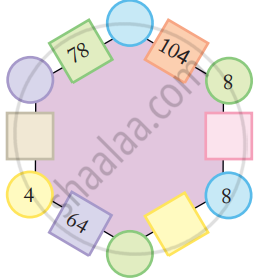
Now you also make your own magic hexagons.
Fill in the blank space in the same way.

The difference of a two-digit number and the number obtained by reversing its digits is always divisible by ______.
A four-digit number abcd is divisible by 11, if d + b = ______ or _____.
If a 3-digit number abc is divisible by 11, then ______ is either 0 or multiple of 11.
Number 7N + 1 will leave remainder 1 when divided by 7.
Fill in the blank space in the same way.

