AO = BO
= 2.9 cm
Advertisements
Advertisements
प्रश्न
Draw a line segment of given length and construct a perpendicular bisector to line segment using scale and compass
58 mm
आकृति
Advertisements
उत्तर
58 mm = `58 xx 1/10` cm = 5.8 cm
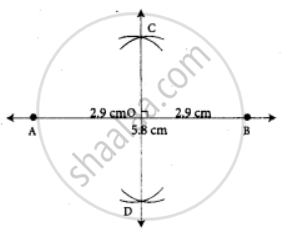
Construction:
Step 1: Drawn a line. Marked two points A and B on it so that
AB = 5.8 cm = 58 mm.
Step 2: Using compass with A as centre and radius more than half of the length of AB, drawn two arcs of the same length one above AB and one below AB.
Step 3: With the same radius and B as centre drawn two arcs to cut the arcs of drawn in step 2.
Marked the points of intersection of the arcs as C and D.
Step 4: Joined C and D. CD intersects AB. Marked the point of intersection as O.
CD is the required perpendicular bisector.
∠AOC = 90°
shaalaa.com
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
APPEARS IN
संबंधित प्रश्न
Draw a line segment AB = 6.2 cm. Mark a point P in AB such that BP = 4 cm. Through point P draw perpendicular to AB.
The line of symmetry of a line segment is the ______ bisector of the line segment.
Only one perpendicular bisector can be drawn to a given line segment.
In the following figure, the point C is the image of point A in line l and line segment BC intersects the line l at P.
- Is the image of P in line l the point P itself?
- Is PA = PC?
- Is PA + PB = PC + PB?
- Is P that point on line l from which the sum of the distances of points A and B is minimum?
Draw a line segment of length 7 cm. Draw its perpendicular bisector, using ruler and compasses.
Draw an angle of 140° with the help of a protractor and bisect it using ruler and compasses.
Bisect a right angle, using ruler and compasses. Measure each part. Bisect each of these parts. What will be the measure of each of these parts?
Draw a line segment of length 12.8 cm. Using compasses, divide it into four equal parts. Verify by actual measurement.
Draw a circle of radius 4 cm. Draw any two of its chords. Construct the perpendicular bisectors of these chords. Where do they meet?
Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of `overline"OA"` and `overline"OB"`. Let them meet at P. Is PA = PB ?
