Advertisements
Advertisements
प्रश्न
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
B - A
उत्तर
B - A =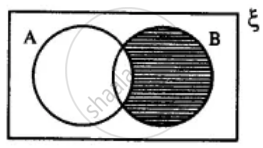
APPEARS IN
संबंधित प्रश्न
Draw a Venn diagram for the truth of the following statement :
All rational number are real numbers.
If A and B are two sets such that \[A \subset B\] then find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C \cup D\]
From the given diagram find :
B - A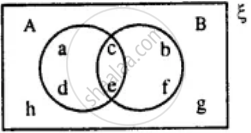
Use the given Venn-diagram to find :
A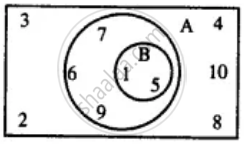
Use the given Venn-diagram to find :
A ∩ B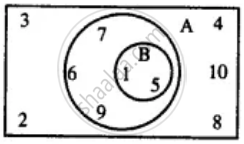
State the sets representing by the shaded portion of following venn-diagram :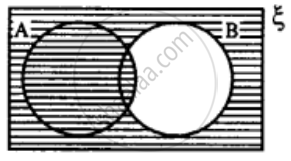
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

