Advertisements
Advertisements
प्रश्न
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

उत्तर
(i) A ∪ B = {a, b, c, d} ∪ {c, d, e, g}
= {a, b, c, d, e, g}
∴ (A ∪ B) - C = {a, b, c, d, e, g} - {b, c, e, f}
= {a, d, g}
(ii) (A ∩ C) = {a, b, c, d} ∩ {b, c, e, f}
= {b, c}
∴ B - (A ∩ C) = {c, d, e, g} - {b, c}
= {d, e, g}
(iii) B ∩ C = {c, e, d, g} ∩ {b, c, e, f}
= {c, e}
∴ A - (B ∩ C) = (A - B) ∪ (A - C)
⇒ (B ∩ C) = {c, e}
So, A − (B ∩ C) = {a, b, d} .....(1)
So, (A − B) ∪ (A − C) = {a, b, d} .....(2)
A − (B ∩ C) = (A − B) ∪ (A − C)
APPEARS IN
संबंधित प्रश्न
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
Draw a Venn diagram for the truth of the following statement :
All rational number are real numbers.
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap C\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - B\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - D\]
Represent the union of two sets by Venn diagram for the following.
P = {a, b, c, e, f} Q = {l, m, n, e, b}
From the given diagram find :
B - A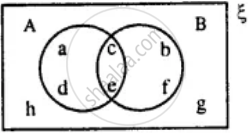
In the given diagram, shade the region which represents the set given underneath the diagrams: (A ∩ B)'
Express the truth of the following statement by the Venn diagram.
Some persons are not politician.
Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming. Draw a Venn diagram showing one of the possible interrelationship among sets U, G, B and S.
