Advertisements
Advertisements
Question
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

Solution
(i) A ∪ B = {a, b, c, d} ∪ {c, d, e, g}
= {a, b, c, d, e, g}
∴ (A ∪ B) - C = {a, b, c, d, e, g} - {b, c, e, f}
= {a, d, g}
(ii) (A ∩ C) = {a, b, c, d} ∩ {b, c, e, f}
= {b, c}
∴ B - (A ∩ C) = {c, d, e, g} - {b, c}
= {d, e, g}
(iii) B ∩ C = {c, e, d, g} ∩ {b, c, e, f}
= {c, e}
∴ A - (B ∩ C) = (A - B) ∪ (A - C)
⇒ (B ∩ C) = {c, e}
So, A − (B ∩ C) = {a, b, d} .....(1)
So, (A − B) ∪ (A − C) = {a, b, d} .....(2)
A − (B ∩ C) = (A − B) ∪ (A − C)
APPEARS IN
RELATED QUESTIONS
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap D\]
Using the Venn diagram, examine the logical equivalence of the following statements:
(a) Some politicians are actors.
(b) There are politicians who are actors.
(c) There are politicians who are not actors.
From the given diagram find :
B - A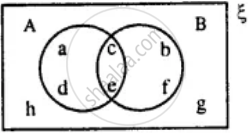
Use the given Venn-diagram to find :
A ∪ B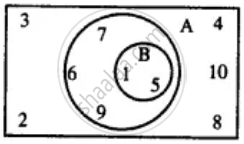
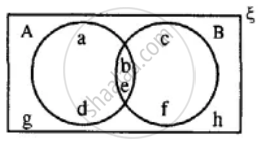
Using the given diagram, express the following sets in the terms of A and B. {a, d, c, f}
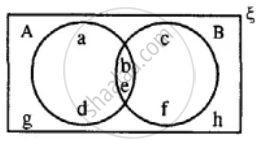
Using the given diagram, express the following sets in the terms of A and B. {a, d, c, f, g, h}
Represent the truth of the following statement by the Venn diagram.
Some hardworking students are obedient.
Represent the truth of the following statement by the Venn diagram.
All teachers are scholars and scholars are teachers.
Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take swimming. Draw a Venn diagram showing one of the possible interrelationship among sets U, G, B and S.
