Advertisements
Advertisements
प्रश्न
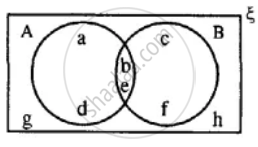
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

उत्तर
(i) A ∪ B = {a, b, c, d} ∪ {c, d, e, g}
= {a, b, c, d, e, g}
∴ (A ∪ B) - C = {a, b, c, d, e, g} - {b, c, e, f}
= {a, d, g}
(ii) (A ∩ C) = {a, b, c, d} ∩ {b, c, e, f}
= {b, c}
∴ B - (A ∩ C) = {c, d, e, g} - {b, c}
= {d, e, g}
(iii) B ∩ C = {c, e, d, g} ∩ {b, c, e, f}
= {c, e}
∴ A - (B ∩ C) = (A - B) ∪ (A - C)
⇒ (B ∩ C) = {c, e}
So, A − (B ∩ C) = {a, b, d} .....(1)
So, (A − B) ∪ (A − C) = {a, b, d} .....(2)
A − (B ∩ C) = (A − B) ∪ (A − C)
APPEARS IN
संबंधित प्रश्न
Draw appropriate Venn diagram for the following:
(A ∪ B)'
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find\[B \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C \cup D\]
Express the truth of each of the following statements using Venn diagrams:
(a) No circles are polygons
(b) Some quadratic equations have equal roots
Use the given Venn-diagram to find :
A ∩ B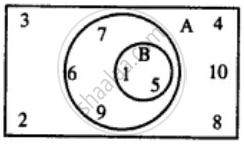
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∩ B
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
(A ∪ B)'
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
B - A
Using the given diagram, express the following sets in the terms of A and B. {a, d}