Selina solutions for Concise Mathematics [English] Class 8 ICSE chapter 6 - Sets [Latest edition]

Write the following set in roster (Tabular) form:

A₁ = {x : 2x + 3 = 11}

Write the following sets in roster (Tabular) form :
A₂ = {x : x² - 4x -5 = 0}

Write the following sets in roster (Tabular) form:

A₃ = {x : x ∈ Z, -3 ≤ x <4}

Write the following sets in roster (Tabular) form :

A₄ = {x : x is a two digit number and sum of digits of x is 7}

Write the following sets in roster (Tabular) form :

A₅ = {x : x = 4n, n ∈ W and n < 4}

Write the following sets in roster (Tabular) form :
A₆ = {x : x = `n/(n+2)`; n ∈ N and n > 5}

Write the following sets in set-builder (Rule Method) form:

B₁ = {6, 9, 12, 15 ....}

Write the following sets in set-builder (Rule Method) form :

B₂ = {11, 13, 7,  19}

Write the following sets in set-builder (Rule Method) form :

B₃ = `{1/3, 3/5, 5/7, 7/9, 9/11, ....}`

Write the following sets in set-builder (Rule Method) form :
B₄ = {8, 27, 64, 125, 216}

Write the following sets in set-builder (Rule Method) form :
B₅ = {-5, -4, -3, -2, -1}

Write the following sets in set-builder (Rule Method) form :
B₆ = {....., -6, -3, 0, 3, 6 ......}

Is {1, 2, 4, 16, 64} = {x : x is a factor of 32}? Give reason.

Is {x : x is a factor of 27} ≠ {3, 9, 27, 54} ? Give reason.

Write the set of even factors of 124.

Write the set of odd factors of 72.

Write the set of prime factors of 3234.

Is {x : x² – 7x + 12 = 0} = {3, 4} ?

Is {x : x² – 5x – 6 = 0} = {2, 3} ?

Write the following sets in Roster form:

The set of letters in the word ‘MEERUT’

Write the following sets in Roster form:

The set of letters in the word ‘UNIVERSAL’.

Write the following sets in Roster form:

A = {x : x = y + 3, y ∈N and y > 3}

Write the following sets in Roster form:

B = {p : p ∈ W and p² < 20}

Write the following sets in Roster form:

C = {x : x is composite number and 5 ≤ x ≤ 21}

List the elements of the following sets:

{x : x² – 2x – 3 = 0}

List the elements of the following sets:

{x : x = 2y + 5; y ∈ N and 2 ≤ y < 6}

List the elements of the following sets:

{x : x is a factor of 24}

List the elements of the following sets:

{x : x ∈ Z and x² ≤ 4}

List the elements of the following sets:

{x : 3x – 2 ≤ 10, x ∈ N}

List the elements of the following sets:

{x : 4 – 2x > -6, x ∈ Z}

Find the cardinal number of the following sets:

A₁ = {-2, -1, 1, 3, 5}

Find the cardinal number of the following sets:

A₂ = {x : x ∈ N and 3 ≤ x <7}

Find the cardinal number of the following sets:

A₃ = {p : p ∈ W and 2P - 3 < 8}

Find the cardinal number of the following sets:

A₄ = {b : b ∈ Z and -7 < 3b -1 ≤ 2}

If P = {P : P is a letter in the word “PERMANENT”}. Find n (P).

State the following sets are finite or infinite:

A = {x : x ∈ Z and x < 10}

State the following sets are finite or infinite:

B = {x : x ∈ W and 5x -3 ≤ 20}

State the following sets are finite or infinite:

P = {y : y = 3x -2, x ∈ N & x > 5}

State the following sets are finite or infinite:

M = {r : r = `3/"n"`; n ∈ W and 6 < n ≤ 15}

Find, if the following sets are singleton sets:

The set of points of intersection of two non-parallel st. lines in the same plane

Find, if the following sets are singleton sets:

A = {x : 7x – 3 = 11}

Find, if the following sets are singleton sets:

B = {y : 2y + 1 < 3 and y ∈ W}

Find, if the following sets are empty:

The set of points of intersection of two parallel lines.

Find, if the following sets are empty:

A = {x : x ∈ N and 5 < x < 6}

Find, if the following sets are empty:

B = {x : x² + 4 = 0, x ∈ N}

Find, if the following sets are empty:

C = {even numbers between 6 & 10}

Find, if the following sets are empty:

D = {prime numbers between 7 & 11}

Are the sets A = {4, 5, 6} and B = {x : x² – 5x – 6 = 0} disjoint?

Are the sets A = {b, c, d, e} and B = {x : x is a letter in the word ‘MASTER’} joint?

State, if the following pair of a set is equivalent or not:

A = {x : x ∈ N and 11 ≥ 2x – 1} and B = {y : y ∈ W and 3 ≤ y ≤ 9}

State, if the following pair of a set is equivalent or not:

Set of integers and set of natural numbers.

State, if the following pair of a set is equivalent or not:

Set of whole numbers and set of multiples of 3.

State, if the following pair of a set is equivalent or not:

P = {5, 6, 7, 8} and M = {x : x ∈ W and x < 4}

State, if the following pair of a set is equal or not :

A = {2, 4, 6, 8} and B = {2n : n ∈ N and n < 5}

State, if the following pair of a set is equal or not :

M = {x : x ∈ W and x + 3 < 8} and N = {y : y = 2n -1, n ∈ N and n < 5}

State, if the following pair of a set is equal or not:

E = {x : x ² + 8x - 9 = 0} and F = {1, - 9} 

State, if the following pair of a set is equal or not:

A = {x : x ∈ N, x < 3} and B = {y : y² - 3y + 2 = 0} 

State if the following set is a finite set or an infinite set:

The set of multiples of 8.

State if the following set is a finite set or an infinite set:

The set of integers less than 10.

State if the following set is a finite set or an infinite set:

The set of whole numbers less than 12.

State if the following set is a finite set or an infinite set:

{x : x = 3n – 2, n ∈ W, n ≤ 8}

State if the following set is a finite set or an infinite set:

{x : x = 3n – 2,n ∈ Z, n ≤ 8}

State if the following set is a finite set or an infinite set:

{x : x = `(n-2)/(n+2)`, n ∈ w)

State the following statement is true or false:

The set of even natural numbers less than 21 and the set of odd natural numbers less than 21 are equivalent sets.

State the following statement is true or false:

If E = {factors of 16} and F = {factors of 20}, then E = F.

State the following statement is true or false:

The set A = {integers less than 20} is a finite set.

State the following statement is true or false:

If A = {x : x is an even prime number}, then set A is empty.

State the following statement is true or false:

The set of odd prime numbers is the empty set.

State the following statement is true or false:

The set of squares of integers and the set of whole numbers are equal sets.

State the following statement is true or false:

In n(P) = n(M), then P → M.

State the following statement is true or false:

If set P = set M, then n(P) = n(M).

State the following statement is true or false:

n(A) = n(B) => A = B.

Find the subset of the following set:

A = {5, 7}

Find the subset of the following set:

B = {a, b, c}

Find the subset of the following set:

C = {x : x ∈ W, x ≤ 2}

Find the subset of the following set:

{p : p is a letter in the word ‘poor’}

If C is the set of letters in the word “cooler”, find: Set C

If C is the set of letters in the word “cooler”, find: n(C)

If C is the set of letters in the word “cooler”, find: The number of its subsets.

If C is the set of letters in the word “cooler”, find: Number of its proper subsets.

If T = {x : x is a letter in the word ‘TEETH’}, find all its subsets.

Given the universal set = {-7,-3, -1, 0, 5, 6, 8, 9}, find: A = {x : x < 2}

Given the universal set = {-7,-3, -1, 0, 5, 6, 8, 9}, find: B = {x : -4 < x < 6}

Given the universal set = {x : x ∈ N and x < 20}, find :
A = {x : x = 3p ; p ∈ N}

Given the universal set = {x : x ∈ N and x < 20}, find:

B = {y : y = 2n + 3, n ∈ N}

Given the universal set = {x : x ∈ N and x < 20}, find:

C = {x : x is divisible by 4}

Find the proper subsets of {x : x² – 9x – 10 = 0}

Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State the following statement is true or false. Give reasons.
A ⊂ B

Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State the following statement is true or false. Give reasons.

B ⊆ A

Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State the following statement is true or false. Give reasons.

C ⊆ B

Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State the following statment is true or false. Give reasons.

B ⊂ A

Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State the following statement is true or false. Give reasons.

C ⊂ A 

Given, A = {Triangles}, B = {Isosceles triangles}, C = {Equilateral triangles}. State the following statement is true or false. Give reasons.

C ⊆ B ⊆ A 

Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State the following statement is true or false. Give reasons.

B ⊂ C

Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State the following statement is true or false. Give reasons.

D ⊂ B

Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State the following statement is true or false. Give reasons.

C ⊆ B ⊆ A

Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State the following statement is true or false. Give reasons. 

D ⊂ A

Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State the following statement is true or false. Give reasons.
B ⊇ C

Given, A = {Quadrilaterals}, B = {Rectangles}, C = {Squares}, D= {Rhombuses}. State the following statement is true or false. Give reasons.

A ⊇ B ⊇ D

Given, universal set = {x : x ∈ N, 10 ≤ x ≤  35}.
A = {x ∈ N : x ≤ 16} Find: A'

Given, universal set = {x : ∈ N, 10 ≤ x ≤ 35}.
B = {x : x > 29} Find: B'. 

Given universal set = {x ∈ Z : -6 < x ≤6}.
N = {n : n is non-negative number}
Find: N'

Given universal set = {x ∈ Z : -6 < x ≤ 6}. P = {x : x is a non-positive number}. Find: P'

Let M = {letters of the word REAL} and N = {letters of the word LARE}. Write sets M and N in roster form and then state whether;
M ⊆ N is true.

Let M = {letters of the word REAL} and N = {letters of the word LARE}. Write sets M and N in roster form and then state whether
N ⊆ M is true.

Let M = {letters of the word REAL} and N = {letters of the word LARE}. Write sets M and N in roster form and then state whether
M = N is true.

Write two sets A and B such that A ⊆ B and B ⊆ A.State the relationship between sets A and B.

Given A = {x : x ∈ N and 3 < x ≤ 6} and B = {x : x ∈ W and x < 4}. Find : Sets A and B in roster form.

Given A = {x : x ∈ N and 3 < x ~ 6} and 8 = {x : x ∈ W and x < 4}. Find: A ∪ B  

Given A = {x : x ∈ N and 3 < x ~ 6} and 8 = {x : x ∈ W and x < 4}. Find: A ∩ B.

Given A = {x : x ∈ N and 3 < x ~ 6} and 8 = {x : x ∈ W and x < 4}. Find: A - B.

Given A = {x : x ∈ N and 3 < x ~ 6} and 8 = {x : x ∈ W and x < 4}. Find: B - A.

If P = {x : x ∈ W and 4 ≤ x ≤ 8}, and Q = {x : x ∈ N and x < 6}. Find: P ∪ Q and P ∩  Q.

If P = {x : x ∈ W and 4 ≤ x ≤ 8}, and Q = {x : x ∈ N and x < 6}. Find: Is (P ∪ Q) ⊃ (P ∩ Q)?

If A = {5, 6, 7, 8, 9}, B = {x : 3 < x < 8 and x ∈ W} and C = {x : x ≤ 5 and x ∈ N}.
Find: A ∪ B and (A ∪ B) ∪ C

If A = {5, 6, 7, 8, 9}, B = {x : 3 < x < 8 and x ∈ W} and C = {x : x ≤ 5 and x ∈ N}. Find:

B ∪ C and A ∪ (B ∪ C)

If A = {5, 6, 7, 8, 9}, B = {x : 3 < x < 8 and x ∈ W} and C = {x : x ≤ 5 and x ∈ N}. Find: 
A ∩ B and (A ∩ B) ∩ C

If A = {5, 6, 7, 8, 9}, B = {x : 3 < x < 8 and x ∈ W} and C = {x : x ≤ 5 and x ∈ N}. Find:

B ∩ C and A ∩ (B ∩  C)
Is (A ∪ B) ∪ C = A ∪ (B ∪ C)?
Is (A ∩ B) ∩ C = A ∩ (B ∩ C)?

Given A = {0, 1, 2, 4, 5}, B = {0, 2, 4, 6, 8} and C = {0, 3, 6, 9}. Show that  A ∪ (B ∪ C) = (A ∪ B) ∪ C i.e. the union of sets is associative.

Given A = {0, 1, 2, 4, 5}, B = {0, 2, 4, 6, 8} and C = {0, 3, 6, 9}. Show that  A ∩ (B ∩ C) = (A ∩ B) ∩ C i.e. the intersection of sets is associative.

If A = {x ∈ W : 5 < x < 10}, B = {3, 4, 5, 6, 7} and C = {x = 2n; n ∈ N and n ≤4}. Find:

A ∩ (B ∪ C)

If A = {x ∈ W : 5 < x < 10}, B = {3, 4, 5, 6, 7} and C = {x = 2n; n ∈ N and n ≤4}. Find:

(B ∪ A) ∩  (B ∪ C)

If A = {x ∈ W : 5 < x < 10}, B = {3, 4, 5, 6, 7} and C = {x = 2n; n ∈ N and n ≤4}. Find:

B ∪ (A ∩ C)

If A = {x ∈ W : 5 < x < 10}, B = {3, 4, 5, 6, 7} and C = {x = 2n; n ∈ N and n ≤4}. Find:

(A ∩  B) ∪ (A ∩ C)

If P = {factors of 36} and Q = {factors of 48}; Find: P ∪ Q

If P = {factors of 36} and Q = {factors of 48}; Find: P ∩ Q

If P = {factors of 36} and Q = {factors of 48}; Find: Q - P.

If P = {factors of 36} and Q = {factors of 48}; Find: P' ∩ Q.

If A = {6, 7, 8, 9}, B = {4, 6, 8,10} and C = {x : x ∈ N : 2 < x ≤ 7};  Find: A -B.

If A = {6, 7, 8, 9}, B = {4, 6, 8,10} and C = {x : x ∈ N : 2 < x ≤ 7}; Find: B - C.

If A = {6, 7, 8, 9}, B = {4, 6, 8,10} and C = {x : x ∈ N : 2 < x ≤ 7}; Find: B - (A - C).

If A = {6, 7, 8, 9}, B = {4, 6, 8,10} and C = {x : x ∈ N : 2 < x ≤ 7};  Find: A - (B ∪ C).

If A = {6, 7, 8, 9}, B = {4, 6, 8,10} and C = {x : x ∈ N : 2 < x ≤ 7};  Find: B - (A ∩ C).

If A = {6, 7, 8, 9}, B = {4, 6, 8,10} and C = {x : x ∈ N : 2 < x ≤ 7};  Find: B - B.

If A = {1, 2, 3, 4, 5}

B = {2, 4, 6, 8}

and C = {3, 4, 5, 6}

Verify : A - (B ∪ C) = (A - B) ∩ (A - C)

If A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8}
and C = {3, 4, 5, 6}
Verify : A - (B ∩ C) = (A - B) ∪ (A - C)

Given A = {x : ∈ N :< 6}, B = {3, 6, 9} and C = {x ∈ N : 2x - 5 ≤ 8}. show that: A ∪ (B ∩ C) = (A ∪  B) ∩ (A ∪ C)

Given A = {x : ∈ N :< 6}, B = {3, 6, 9} and C {x ∈ N : 2x - 5 ≤ 8}. show that: A ∩ (B ∪ C) = (A ∩  B) ∪ (A ∩ C)

From the given diagram find : 
A ∪ B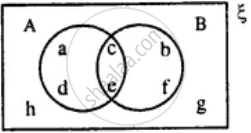

From the given diagram find : 
A' ∩ B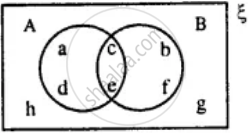

From the given diagram find : 
A - B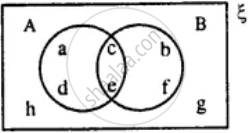

From the given diagram find : 
B - A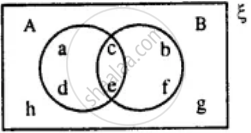

From the given diagram find : 
(A ∪ B)'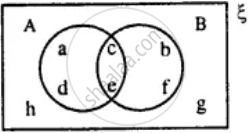

From the given diagram, find: 
(i) A’ 
(ii) B’ 
(iii) A' ∪ B' 
(iv) (A ∩ B)'

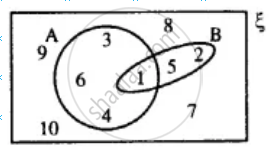
Is A' ∪ B' = (A ∩ B)' ?

Also, verify if A' ∪ B' = (A ∩ B)'.

Use the given diagram to find:

(i) A ∪ (B ∩ C)

(ii) B - (A - C)

(iii) A - B

(iv) A ∩ B'

Is A ∩ B' = A - B?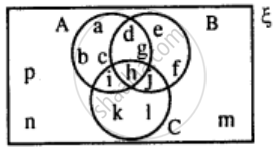

Use the given Venn-diagram to find: 
B - A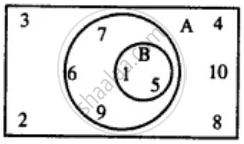

Use the given Venn-diagram to find :
A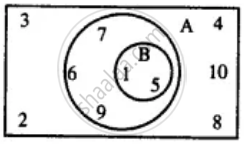

Use the given Venn-diagram to find :
B'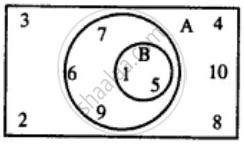

Use the given Venn-diagram to find :
A ∩ B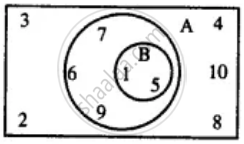

Use the given Venn-diagram to find :
A ∪ B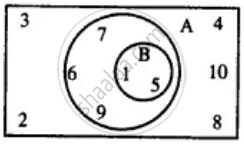

Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∩ B

Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∪ B

Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
B - A

Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∪ B

Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
B' ∩ A

Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
A ∩ B

Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
(A ∪ B)'

Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
A ∪ B

Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
(A ∪ B)'

Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
B - A

Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
B ∩ A'

State the sets representing by the shaded portion of following venn-diagram :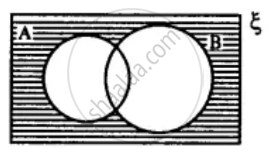

State the sets representing by the shaded portion of following venn-diagram :

State the sets representing by the shaded portion of following venn-diagram :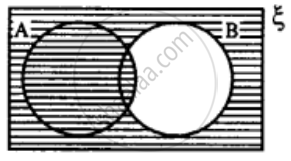

In the given diagram, shade the region which represents the set given underneath the diagrams: (B - A)'

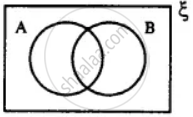
In the given diagram, shade the region which represents the set given underneath the diagrams: (A ∩ B)'

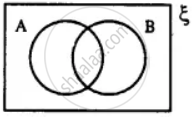
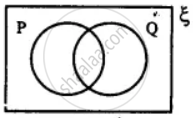
In the given diagram, shade the region which represents the set given underneath the diagrams: (P ∩ Q)'

From the given diagram, find :
(i) (A ∪ B) - C

(ii) B - (A ∩ C)

(iii) (B ∩ C) ∪ A

Verify :
A - (B ∩ C) = (A - B) ∪ (A - C) 

Using the given diagram, express the following sets in the terms of A and B. {a, d}

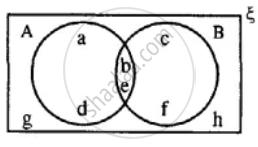
Using the given diagram, express the following sets in the terms of A and B. {a, d, c, f}

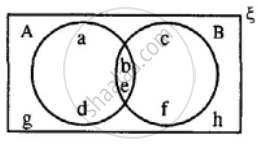
Using the given diagram, express the following sets in the terms of A and B. {a, d, c, f, g, h}

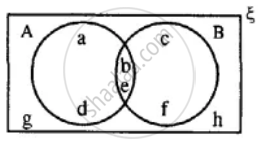
Using the given diagram, express the following sets in the terms of A and B. {a, d, g, h}

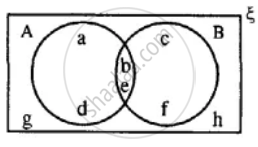
Using the given diagram, express the following sets in the terms of A and B. {g, h}