Advertisements
Advertisements
Question
From the given diagram, find:
(i) A’
(ii) B’
(iii) A' ∪ B'
(iv) (A ∩ B)'
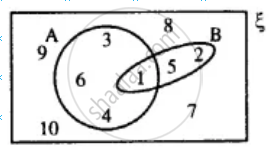
Is A' ∪ B' = (A ∩ B)' ?
Also, verify if A' ∪ B' = (A ∩ B)'.
Solution
(i) A = {1, 3, 4, 6}
A' = {2, 5, 7, 8, 9, 10}
(ii) B = {1, 2, 5}
∴ B' = {3, 4, 6, 7, 8, 9, 10}
(iii) A' ∪ B' = {2, 5, 7, 8, 9, 10} ∪ {3, 4, 6, 7, 8, 9, 10}
= {2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) A ∩ B = {1, 3, 4, 6} ∩ {1, 2, 5}
= {1}
∴ (A ∩ B)' = {2, 3, 4, 5, 6, 7, 8, 9, 10}
From Part (iii) and Part (iv) we conclude
A' ∪ B' = (A ∩ B)'
Now A ∩ B = {2, 5, 7, 8, 9, 10} ∩ {3, 4, 6, 7, 8, 9, 10}
⇒ A' ∪ B' = {7, 8, 9, 10} ...(I)
Now A ∪ B = {1, 3, 4, 6} ∪ {1, 2, 5}
= {1, 2, 3, 4, 5, 6}
∴ (A ∩ B)' = {7, 8, 9, 10} ...(II)
From I and II we conclude
A' ∪ B' = (A ∩ B)'
APPEARS IN
RELATED QUESTIONS
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[B \cup C \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cup D \right) \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap C\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap D\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - C\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find:
\[B - A\]
Express the truth of each of the following statements by Venn diagram :
(a) Some hardworking students are obedient.
(b) No circles are polygons.
(c) All teachers are scholars and scholars are teachers.
Use the given Venn-diagram to find :
B'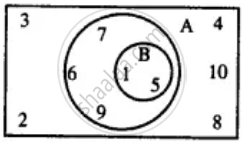
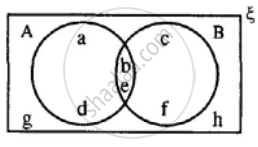
Using the given diagram, express the following sets in the terms of A and B. {a, d, g, h}
Represent the truth of the following statement by the Venn diagram.
All teachers are scholars and scholars are teachers.
