Advertisements
Advertisements
Question
Use the given diagram to find:
(i) A ∪ (B ∩ C)
(ii) B - (A - C)
(iii) A - B
(iv) A ∩ B'
Is A ∩ B' = A - B?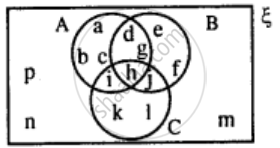
Solution
(i) B ∩ C = {d, e, f, g, h,j} ∩ {h, i, j, k, l}
= {h, j}
∴ A ∪ (B ∩ C) = {a, b, c, d, g, h, i} ∪ {h, j}
= {a, b, c, d, g, h, i, j}
(ii) A - C = {a, b, c, d, g, h, i} - {h, i, j, k, l}
= {a, b, c, d, g}
∴ B - (A - C) = {d, e, f, g, h, j} - {a, b, c, d, g}
= {e, f, h, j}
(iii) A - B = {a, b, c, d, g, h, i} - {d, e, f, g, h, j}
⇒ A - B = {a, b, c, i} ...(I)
(iv) B' = {a, b, c ,i, k, l, m, n, p}
A ∩ B' = {a, b, c, d, g, h, i} ∩ {a, b, c, i, k, l, m, n, p}
⇒ A ∩ B' = {a, b, c, i} ...(II)
From I and II we can conclude A ∩ B' = A - B
APPEARS IN
RELATED QUESTIONS
Draw appropriate Venn diagram for the following:
A' ∩ B'
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cup D \right) \cap \left( B \cup C \right)\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}.
Find: \[B - D\]
Represent the union of two sets by Venn diagram for the following.
A = {3, 4, 5, 7} B = {1, 4, 8}
Express the truth of the following statements with the help of Venn diagram:
(a) No circles are polygon
(b) If a quadrilateral is rhombus , then it is a parallelogram .
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
A ∪ B
Represent the truth of the following statement by the Venn diagram.
No circles are polygons.
Represent the following statement by the Venn diagram.
No circle is rectangle.
Express the truth of the following statement by the Venn diagram.
All men are mortal.
