Advertisements
Advertisements
प्रश्न
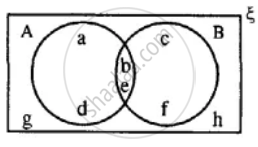
Use the given diagram to find:
(i) A ∪ (B ∩ C)
(ii) B - (A - C)
(iii) A - B
(iv) A ∩ B'
Is A ∩ B' = A - B?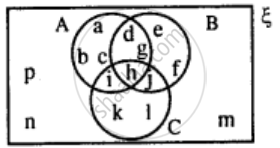
उत्तर
(i) B ∩ C = {d, e, f, g, h,j} ∩ {h, i, j, k, l}
= {h, j}
∴ A ∪ (B ∩ C) = {a, b, c, d, g, h, i} ∪ {h, j}
= {a, b, c, d, g, h, i, j}
(ii) A - C = {a, b, c, d, g, h, i} - {h, i, j, k, l}
= {a, b, c, d, g}
∴ B - (A - C) = {d, e, f, g, h, j} - {a, b, c, d, g}
= {e, f, h, j}
(iii) A - B = {a, b, c, d, g, h, i} - {d, e, f, g, h, j}
⇒ A - B = {a, b, c, i} ...(I)
(iv) B' = {a, b, c ,i, k, l, m, n, p}
A ∩ B' = {a, b, c, d, g, h, i} ∩ {a, b, c, i, k, l, m, n, p}
⇒ A ∩ B' = {a, b, c, i} ...(II)
From I and II we can conclude A ∩ B' = A - B
APPEARS IN
संबंधित प्रश्न
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[A \cap C\]
Using the Venn diagram, examine the logical equivalence of the following statements:
(a) Some politicians are actors.
(b) There are politicians who are actors.
(c) There are politicians who are not actors.
Express the truth of each of the following statements by Venn diagram :
(a) Some hardworking students are obedient.
(b) No circles are polygons.
(c) All teachers are scholars and scholars are teachers.
Use the given Venn-diagram to find:
B - A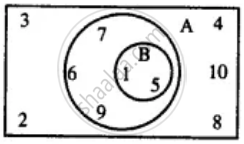
Use the given Venn-diagram to find :
A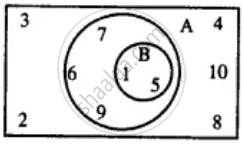
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
B' ∩ A
In the given diagram, shade the region which represents the set given underneath the diagrams: (P ∩ Q)'
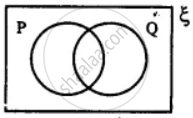
Using the given diagram, express the following sets in the terms of A and B. {a, d}
Represent the following statement by the Venn diagram.
No circle is rectangle.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
All the students who study Mathematics study English, but some students who study English do not study Mathematics.
