Advertisements
Advertisements
प्रश्न
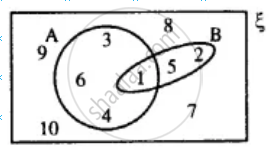
From the given diagram, find:
(i) A’
(ii) B’
(iii) A' ∪ B'
(iv) (A ∩ B)'
Is A' ∪ B' = (A ∩ B)' ?
Also, verify if A' ∪ B' = (A ∩ B)'.
उत्तर
(i) A = {1, 3, 4, 6}
A' = {2, 5, 7, 8, 9, 10}
(ii) B = {1, 2, 5}
∴ B' = {3, 4, 6, 7, 8, 9, 10}
(iii) A' ∪ B' = {2, 5, 7, 8, 9, 10} ∪ {3, 4, 6, 7, 8, 9, 10}
= {2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) A ∩ B = {1, 3, 4, 6} ∩ {1, 2, 5}
= {1}
∴ (A ∩ B)' = {2, 3, 4, 5, 6, 7, 8, 9, 10}
From Part (iii) and Part (iv) we conclude
A' ∪ B' = (A ∩ B)'
Now A ∩ B = {2, 5, 7, 8, 9, 10} ∩ {3, 4, 6, 7, 8, 9, 10}
⇒ A' ∪ B' = {7, 8, 9, 10} ...(I)
Now A ∪ B = {1, 3, 4, 6} ∪ {1, 2, 5}
= {1, 2, 3, 4, 5, 6}
∴ (A ∩ B)' = {7, 8, 9, 10} ...(II)
From I and II we conclude
A' ∪ B' = (A ∩ B)'
APPEARS IN
संबंधित प्रश्न
If A and B are two set such that \[A \subset B\]then find:
\[A \cap B\]
If A and B are two sets such that \[A \subset B\] then find:
\[A \cup B\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - B\]
From the given diagram find :
A ∪ B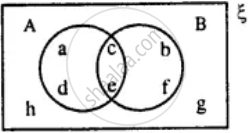
From the given diagram find :
B - A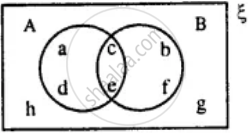
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

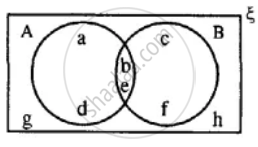
Using the given diagram, express the following sets in the terms of A and B. {a, d}
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
Some of the students study Mathematics but do not study English, some study English but do not study Mathematics, and some study both.
Draw the Venn diagrams to illustrate the following relationship among sets E, M and U, where E is the set of students studying English in a school, M is the set of students studying Mathematics in the same school, U is the set of all students in that school.
Not all students study Mathematics, but every students studying English studies Mathematics.
Draw Venn diagram for the following:
Some students are not scholars
