Advertisements
Advertisements
प्रश्न
Draw a ∆ABC in which base BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are \[\frac{3}{4}\] of the corresponding sides of ∆ABC.
उत्तर
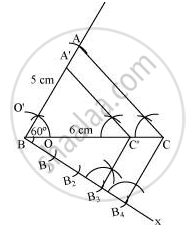
ΔA'BC' whose sides are `3/2`of the corresponding sides of ΔABC can be drawn as follows.
Step 1 Draw a ΔABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
Step 2 Draw a ray BX making an acute angle with BC on the opposite side of vertex A.
Step 3 Locate 4 points (as 4 is greater in 3 and 4), B1, B2, B3, B4, on line segment BX.
Step 4 Join B4C and draw a line through B3, parallel to B4C intersecting BC at C'.
Step 5 Draw a line through C' parallel to AC intersecting AB at A'. ΔA'BC' is the required triangle.
Justification
The construction can be justified by proving
`A'B = 3/4 AB, BC' = 3/4 BC , A'C' = 3/4 AC`
In ΔA'BC' and ΔABC,
∠A'C'B = ∠ACB (Corresponding angles)
∠A'BC' = ∠ABC (Common)
∴ ΔA'BC' ∼ ΔABC (AA similarity criterion)
⇒ `(A'B)/(AB) = (BC')/(BC) = (A'C')/(AC) `… (1)
In ΔBB3C' and ΔBB4C,
∠B3BC' = ∠B4BC (Common)
∠BB3C' = ∠BB4C (Corresponding angles)
∴ ΔBB3C' ∼ ΔBB4C (AA similarity criterion)
⇒`(BC')/(BC) = (BB_3)/(BB_4)`
⇒`(BC') / (BC) = 3/4 ....... (2)`
From equations (1) and (2), we obtain
`(A'B)/(AB) = (BC')/(BC) = (A'C')/(AC) = 3/4`
⇒`A'B = 3/4 AB, BC' = 3/4 BC , A'C' = 3/4 AC`
APPEARS IN
संबंधित प्रश्न
Construct a right triangle ABC with AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD, the perpendicular from B on AC. Draw the circle through B, C and D and construct the tangents from A to this circle.
Construct an isosceles triangle whose base is 6 cm and altitude 4 cm. Then construct another triangle whose sides are `3/4`times the corresponding sides of the isosceles triangle.
Draw a triangle ABC with BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are `3/4` of the corresponding sides of the ∆ABC.
Construct a ΔPQR , in which PQ = 6 cm, QR = 7 cm and PR =- 8 cm. Then, construct another triangle whose sides are`4/5` times the corresponding sides of ΔPQR .
Construct a ΔABC with BC = 7 cm, ∠B = 60° and AB = 6 cm. Construct another triangle whose sides are `3/4` times the corresponding sides of ΔABC
Construct a ΔABC in which AB = 6 cm, ∠A = 30° and ∠AB = 60° . Construct another ΔAB'C ' similar to ΔABC with base AB’ = 8 cm.
Construct a ΔABC in which BC = 8 cm, ∠B = 45° and ∠C = 60° . Construct another triangle similar to ΔABC such that its sides are `3/5`of the corresponding sides of ΔABC .
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3cm. Then, construct another triangle whose sides are `5/3`times the corresponding sides of the given triangle.
Draw a triangle ABC with BC = 7 cm, ∠ B = 45° and ∠C = 60°. Then construct another triangle, whose sides are `3/5` times the corresponding sides of ΔABC.
Construct a triangle PQR with sides QR = 7 cm, PQ = 6 cm and \[\angle\]PQR = 60º. Then construct another triangle whose sides are \[\frac{3}{5}\] of the corresponiding sides of ∆PQR.
