Advertisements
Advertisements
प्रश्न
एक बेलन 30° कोण बनाते आनत तल पर लुढ़कता हुआ ऊपर चढ़ता है। आनत तल की तली में बेलन के द्रव्यमान केन्द्र की चाल 5 m/s है।
- आनत तल पर बेलन कितना ऊपर जाएगा?
- वापस तली तक लौट आने में इसे कितना समय लगेगा?
उत्तर
(a) ऊर्जा संरक्षण सिद्धांत से बेलन के ऊपर चढ़ने पर,
गतिज ऊर्जा में कमी = स्थितिज ऊर्जा में वृद्धि
अर्थात `1/2 "Mν"_"cm"^2 + 1/2 "Iω"^2 = "Mgh"` ...(1)
ठोस बेलन का जड़त्व आघूर्ण `"I" = 1/2 "MR"^2`
तथा बिना फिसले लुढ़कने के लिए
`"ν"_"cm" = "Rω" => "ω"_0 = "ν"_"cm"/"R"`
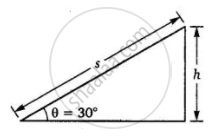
एवं चित्र से,
h = s sin 30° = s/2
अतः समीकरण (1) में ये मान रखने पर,
`1/2 "Mν"^2"cm" 1/2 (1/2"MR"^2)("ν"_"cm"/"R")^2 = "Mg"("s"/2)`
`3/4 "Mν"_"cm"^2 = 1/2 "Mgs"`
`=> "s" = (3 "ν" "cm"^2)/(2"g")`
`= (3(5)^2)/(2 xx 9.8)` m
= 3.8 m
आनत ताल पर मंदन, `"a" = ("g" "sin" theta)/(1 + ("K"^2/"R"^2))`
परन्तु बेलन के लिए `1/2"MR"^2 = "MK"^2`
`"K"^2/"R"^2 = 1/2 ` तथा θ = 30°
`"a" = ("g" "sin" 30^circ)/(1 + 1/2) = ("g" xx (1//2))/(3//2) = "g"/3`
अतः सूत्र `"s" = "ut" + 1/2 "at"^2` से,
`"a" = 5 xx "t" + 1/2(- "g"/3) . "t"^2`
सरल करने पर, t =`(30/"g")` सेकंड = `(30/9.8)` सेकंड = 3.06 सेकंड ≈ 3 सेकंड
APPEARS IN
संबंधित प्रश्न
एकसमान द्रव्यमान घनत्व के निम्नलिखित पिण्डों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए:
- गोला
- सिलिंडर
- छल्ला तथा
- घन।
क्या किसी पिण्ड का द्रव्यमान केंद्र आवश्यक रूप से उस पिण्ड के भीतर स्थित होता है?
HCl अणु में दो परमाणुओं के नाभिकों के बीच पृथकन लगभग 1.27 A (1Å = 10-10 m) है। इस अणु के द्रव्यमान केंद्र की लगभग अवस्थिति ज्ञात कीजिए। यह ज्ञात है कि क्लोरीन का परमाणु हाइड्रोजन के परमाणु की तुलना में 35.5 गुना भारी होता है तथा किसी परमाणु का समस्त द्रव्यमान उसके नाभिक पर केंद्रित होता है।
कोई बच्चा किसी चिकने क्षैतिज फर्श पर एकसमान चाल ν से गतिमान किसी लंबी ट्रॉली के एक सिरे पर बैठा है। यदि बच्चा खड़ा होकर ट्रॉली पर किसी भी प्रकार से दौड़ने लगता है, तब निकाय (ट्रॉली + बच्चा) के द्रव्यमान केंद्र की चाल क्या है?
3 kg द्रव्यमान तथा 40 cm त्रिज्या के किसी खोखले सिलिंडर पर कोई नगण्य द्रव्यमान की रस्सी लपेटी गई है। यदि रस्सी को 30 N बल से खींचा जाए तो सिलिंडर का कोणीय त्वरण क्या होगा। रस्सी का रैखिक त्वरण क्या है? यह मानिए कि इस प्रकरण में कोई फिसलन नहीं है।
एक मीटर छड़ के केन्द्र के नीचे क्षुर-धार रखने पर वह इस पर संतुलित हो जाती है जब दो सिक्के, जिनमें प्रत्येक का द्रव्यमान 5 g है, 12.0 cm के चिह्न पर एक के ऊपर एक रखे जाते हैं तो छड़ 45.0 cm चिह्न पर संतुलित हो जाती है। मीटर छड़ का द्रव्यमान क्या है?
